Vektor-Subtraktion

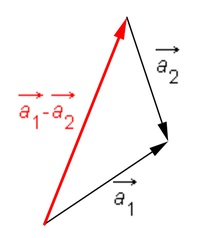
Vektorsubtraktion

: Abb. 1: Vektorsubtraktion
zweier Vektoren

Die Vektorsubtraktion eines Vektors a₂ von einem Vektor a₁ ist die Umkehrfunktion zur Vektoraddition. Sie entspricht der Addition des Vektors a₂ mit umgekehrter Orientierung.

$\vec{a_1}-\vec{a_2}$

Vektorsubtraktion - Grafisch

Grafisch wird eine Vektorsubtraktion realisiert, indem an die Spitze des ersten Vektors die Spitze des zweiten Vektors gesetzt wird (Siehe Abb. 1).

Vektoraddition - Rechnerisch

Rechnerisch erfolgt die Vektorsubtraktion, indem man die x-Werte und die y-Werte jeweils von einander subtrahiert.

Vektorsubtraktion in der Ebene

$\vec{a_1}=\left(\begin{array}{r}3\\5\end{array}\right)$

$\vec{a_2}=\left(\begin{array}{r}8\\4\end{array}\right)$

$\vec{a_{ges}}=\vec{a_1}-\vec{a_2}=\left(\begin{array}{r}3\\5\end{array}\right)-\left(\begin{array}{r}8\\4\end{array}\right)$

$\vec{a_{ges}}=\left(\begin{array}{r}3-8\\5-4\end{array}\right)=\left(\begin{array}{r}-5\\1\end{array}\right)$

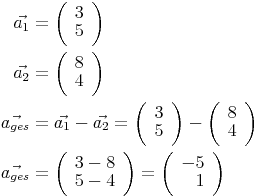
Die allgemeine Formel zur Subtraktion zweier Vektoren in $\mathbb{R}^2$ lautet:

$\vec{a_1}-\vec{a_2}=\left(\begin{array}{r}x_1\\y_1\end{array}\right)-\left(\begin{array}{r}x_2\\y_2\end{array}\right)=\left(\begin{array}{rrr}x_1&-&x_2\\y_1&-&y_2\end{array}\right)$

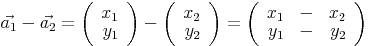
Vektorsubtraktion im Raum

$\vec{a_1}=\left(\begin{array}{r}2\\-1\\3\end{array}\right)$

$\vec{a_2}=\left(\begin{array}{r}-4\\-3\\2\end{array}\right)$

$\vec{a_{ges}}=\vec{a_1}-\vec{a_2}=\left(\begin{array}{r}2\\-1\\3\end{array}\right)-\left(\begin{array}{r}-4\\-3\\2\end{array}\right)$

$\vec{a_{ges}}=\left(\begin{array}{rrr}2&-&(-4)\\(-1)&-&(-3)\\3&-&2\end{array}\right)=\left(\begin{array}{r}6\\2\\1\end{array}\right)$

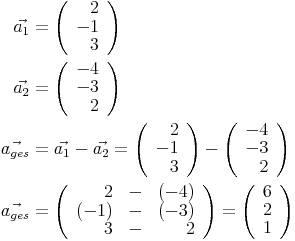
Die allgemeine Formel zur Subtraktion zweier Vektoren in $\mathbb{R}^3$ lautet:

$\vec{a_1}-\vec{a_2}=\left(\begin{array}{r}x_1\\y_1\\z_1\end{array}\right)-\left(\begin{array}{r}x_2\\y_2\\z_2\end{array}\right)=\left(\begin{array}{rrr}x_1&-&x_2\\y_1&-&y_2\\z_1&-&z_2\end{array}\right)$

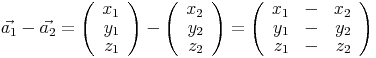
Dieser Artikel hat mir geholfendas half mir
Dieser Artikel hat mir nicht geholfen... leider nicht
Kommentar zu dieser Seite abgebenKommentar
Frage im Forum stellenForum
Offizielle Facebook-SeiteFacebook

Kommentar schreiben

Kommentare zu diesem Thema