Abb. 1: Ungebundener VektorVektor und Vektorklassen
Ungebundener Vektor
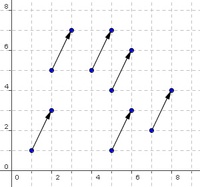
Ein Vektor ist an sich an keinen Ort gebunden. Er gibt nur eine Verschiebung um einen bestimmten Wert in eine bestimmte Richtung an. Das bedeutet, dass dieser Vektor an jeder Stelle auftreten kann.
Die in Abb. 1 gezeigten Vektoren sind alle gleich und sind eigentlich nur einige wenige Repräsentanten einer Vektorklasse - nämlich der Vektorklasse
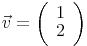
Man spricht hierbei auch von einem ungebundenen Vektor.
Klarerweise gibt es unendlich viele Möglichkeiten, wo ein ungebundener Vektor (= eine Verschiebung) angewendet werden kann.
Abb. 2: Gebundener VektorGebundener Vektor
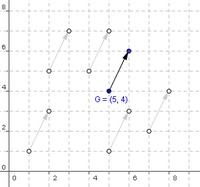
Wird zum Vektor auch noch ein Anfangspunkt festgelegt, legt man einen eindeutig festgelegten Vektor einer ganzen Vektorklasse fest.
Man spricht somit von einem gebundenen Vektor, da dieser Vektor an eine bestimmte Position gebunden ist.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
fruchtigerApfel
sehr gut erklärt! :D