Darstellung von ganzen Zahlen auf der Zahlengeraden
Die Menge der natürlichen Zahlen reicht für viele Rechnungen nicht mehr aus. Zum Beispiel ist die Subtraktion 3 - 10 = in der Menge der natürlichen Zahlen nicht mehr lösbar.
Aus diesem Grunde erweitern wir die natürlichen Zahlen auf die Menge der ganzen Zahlen.
Die Menge der ganzen Zahlen wird mit dem Symbol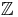 
abgekürzt.
Wir erweitern also den Zahlenstrahl der natürlichen Zahlen bei 0 nach links. Dadurch entsteht eine Zahlengerade.
Jene Zahlen, die kleiner als 0 sind liegen auf der Zahlengeraden links der Zahl 0. Sie werden als negative ganze Zahlen bezeichnet, ihr Vorzeichen ist ein -.
Jene Zahlen, die größer als 0 sind liegen auf der Zahlengeraden rechts der Zahl 0. Sie werden als positive ganze Zahlen bezeichnet, ihr Vorzeichen ist ein +.
Die Menge der ganzen Zahlen
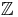setzt sich aus den negativen ganzen Zahlen (
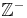), der Zahl 0 und den positiven ganzen Zahlen (
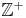) zusammen.Auf der Zahlengeraden werden die ganzen Zahlen als Punkt dargestellt.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar