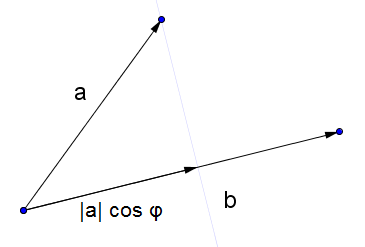
Skalares Produkt

Skalares Produkt

Das skalare Produkt (inneres Produkt) lässt sich mit folgender Beziehung beschreiben:

Definition:
$\langle a, b \rangle = a \cdot b = \left| a \right| \left| b \right| \cos \varphi$

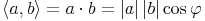
Einige Anmerkungen dazu:

Bilden die beiden Vektoren einen spitzen Winkel, so ist das Ergebnis positiv
Bilden die beiden Vektoren einen stumpfen Winkel, so ist das Ergebnis negativ
Stehen die beiden Vektoren normal zueinander, so ist das Ergebnis 0

Berechnung des skalaren Produkts

Das skalare Produkte kann mit folgender Rechenvorschrift ermittelt werden:

a) Berechnung des skalaren Produkts in der Ebene:

$\begin{pmatrix} x_1 \\ y_1 \end{pmatrix} \cdot \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} = x_1 \cdot x_2 + y_1 \cdot y_2$

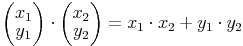
b) Berechnung des skalaren Produkts im Raum:

$\begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} \cdot \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} = x_1 \cdot x_2 + y_1 \cdot y_2 + z_1 \cdot z_2$

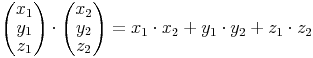
Beispiele zum skalaren Produkt

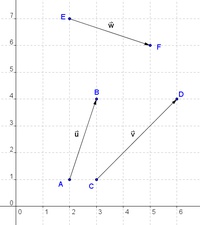
Im folgenden Beispiel soll der Winkel zwischen den Vektoren

$\vec{u}, \vec{v}, \vec{w}$

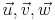
ermittelt werden. Zuerst ermitteln wir die oben genannten Vektoren:

$\begin{align} & \vec{u} = B - A = \begin{pmatrix} 3 \\ 4 \end{pmatrix} - \begin{pmatrix} 2 \\ 1 \end{pmatrix} = \begin{pmatrix} 1 \\ 3 \end{pmatrix} \\ & \vec{v} = D - C = \begin{pmatrix} 6 \\ 4 \end{pmatrix} - \begin{pmatrix} 3 \\ 1 \end{pmatrix} = \begin{pmatrix} 3 \\ 3 \end{pmatrix} \\ & \vec{w} = F - E = \begin{pmatrix} 5 \\ 6 \end{pmatrix} - \begin{pmatrix} 2 \\ 7 \end{pmatrix} = \begin{pmatrix} 3 \\ -1 \end{pmatrix} \end{align}$

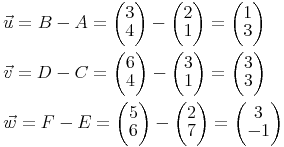
Beispiel 1:

Der Winkel zwischen Vektor u und v soll ermittelt werden. Es werden die entsprechenden Vektoren eingesetzt. Auf der linken Seite der Gleichung wird das skalare Produkt angewendet, auf der rechten Seite können die Beträge der Vektoren ermittelt werden. Somit ist die einzige unbekannte Variable der Winkel. Durch Umformen kann dieser schließlich berechnet werden.

$\begin{alignat}{2} \vec{u} \cdot \vec{v} & = | \vec{u} | \cdot | \vec{v} | \cdot \cos \varphi \\ \begin{pmatrix} 1 \\ 3 \end{pmatrix} \cdot \begin{pmatrix} 3 \\ 3 \end{pmatrix} & = \left| \begin{pmatrix} 1 \\ 3 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 3 \\ 3 \end{pmatrix} \right| \cdot \cos \varphi \\ 1 \cdot 3 + 3 \cdot 3 & = \sqrt{1^2 + 3^2} \sqrt{3^2 + 3^2} \cos \varphi \\ 12 & = \sqrt{10} \cdot \sqrt{18} \cos \varphi && :\sqrt{10}:\sqrt{18} \\ \frac{12}{ \sqrt{10} \sqrt{18} } & = \cos \varphi \\ \cos \varphi & = 0,89442719099... && \cos^{-1} \\ \varphi & = 26,56505117 ... \\ \varphi & \approx 26,57^\circ \\\end{alignat}$

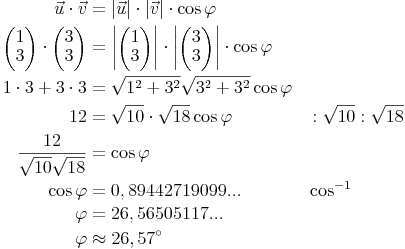
Beispiel 2:

Dies ist ein ähnliches Beispiel, jedoch sind in diesem Fall die beiden Vektoren normal zueinander. In diesem Fall erkennt man, dass das skalare Produkt bereits 0 ergibt. cos^-1 von 0 ergibt natürlich 90 Grad. Um zwei Vektoren auf normale Lage zu prüfen, muss somit lediglich geprüft werden, ob das skalare Produkt null ergibt.

$\begin{alignat}{2} \vec{u} \cdot \vec{v} & = | \vec{u} | \cdot | \vec{v} | \cdot \cos \varphi \\ \begin{pmatrix} 1 \\ 3 \end{pmatrix} \cdot \begin{pmatrix} 3 \\ -1 \end{pmatrix} & = \left| \begin{pmatrix} 1 \\ 3 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 3 \\ -1 \end{pmatrix} \right| \cdot \cos \varphi \\ 1 \cdot 3 + 3 \cdot (-1) & = \sqrt{1^2 + 3^2} \sqrt{3^2 + (-1)^2} \cos \varphi \\ 0 & = \sqrt{10} \cdot \sqrt{10} \cos \varphi \\ 0 & = 10 \cdot \cos \varphi && : 10 \\ 0 & = \cos \varphi && \cos^{-1} \\ \varphi & = 90^\circ \\ \end{alignat}$

Merke: Ist das skalare Produkt zweier Vektoren null, so stehen die beiden Vektoren normal zueinander.

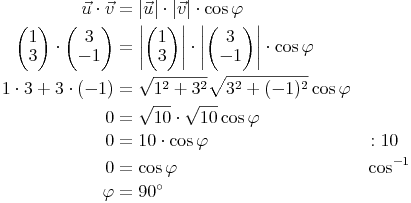
Dieser Artikel hat mir geholfen. das half mir
... leider nicht ... leider nicht
Kommentar Kommentar
4,0
16 Bewertungen

Skalares Produkt