Differentialquotient

Der Differentialquotient an der Stelle x0 entsteht durch die Bildung des Grenzwertes des Differenzenquotienten zwischen x1 und x0, wobei x1 gegen x0 strebt.

Vom Differenzenquotient zum Differentialquotient

Der Differenzenquotient entspricht dem Quotient aus Gegenkathete und Ankathete des entsprechenden Steigungsdreiecks zwischen zwei Punkten.

Versucht man nun die Steigung zwischen ein und dem selben Punkt zu ermitteln wird man kläglich scheitern. Hat man beispielsweise einen Punkt (P) einer Funktion mit x=5 und f(x)=3, so führt der Differenzenquotient zwischen P und P zu:

\frac{f(x)-f(x)}{x-x}\ =\ \frac{3-3}{5-5}\ =\ \frac{0}{0}\ \Rightarrow\ \mbox{nicht lösbar!}

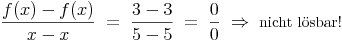
Annäherung durch Bildung des Grenzwertes

Da man durch Verwendung ein und des selben Punktes nicht zu einer Lösung kommt, muss man sich von einer Seite an diesen Punkt nähern. Durch Bildung des Grenzwertes lässt man den x-Wert des zweiten Punktes gegen den x-Wert des ersten Punktes und somit den Abstand gegen Null streben, wodurch man letztendlich die Steigung der Tangente erhält.

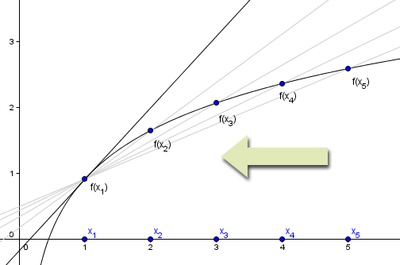Tangente, Grenzwertbildung Grenzwertbildung

In der oben angeführten Abbildung sind fünf Punkte P1, P2, P3, P4 und P5 abgebildet. Je näher sich der Punkt Pn beim Punkt P1 befindet desto näher ist die Steigung der Sekante bei der Steigung der Tangente von P1.

Lässt man diesen Abstand unendlich klein werden, so erhält man die Steigung der Tangente. Somit gilt:

Der Differentialquotient ist der Grenzwert des Differenzenquotienten, wobei x2 gegen x1 strebt.

\lim_{x_2 \to x_1}\frac{f(x_2)-f(x_1)}{x_2-x_1}

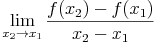
In diesem Fall nennt man dies die erste Ableitung f'(x1) der Funktion f an der Stelle x1.

Die erste Ableitung einer Funktion f an der Stelle x1 lautet:

f'(x_1)\ =\ \lim_{x_2 \to x_1}\frac{f(x_2)-f(x_1)}{x_2-x_1}
Anmerkung:

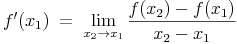
Voraussetzung ist, dass die Funktion f an der Stelle x1 differenzierbar ist.

Kommentar #425 von Klaus Rindfrey 10.06.11 08:11
Klaus Rindfrey

In der "Anmerkung" heißt es:

"Voraussetzung ist, dass die Funktion f an der Stelle x1 differenzierbar ist. Dies ist gegeben, wenn die Funktion f an der Stelle x1 stetig ist."

Das ist falsch. Aus der Stetigkeit folgt nicht die Diffenrenzierbarkeit.

Beispiel:

Die Betragsfunktion f(x)=|x| ist an der Stelle x=0 stetig, aber nicht differenzierbar.

Umgekehrt wäre es richtig: Aus der Differenzierbarkeit folgt die Stetigkeit.

Kommentar #426 von admin 10.06.11 15:44
admin

Danke für den Hinweis. Der Fehler wurde bereits behoben

Kommentar verfassen