Satz von Thales

Der Satz von Thales

Beispiel:

Konstruieren Sie über der Strecke 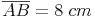$\overline{AB} = 8\ cm$ einen Halbkreis. Wählen Sie zumindest 3 beliebige Punkte auf dem Kreisbogen und benennen Sie diese mit 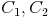C_1, C_2 und C_3 .

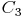Versuchen Sie anhand dieses Beispiels eine Besonderheit herauszufinden! Da es sich um 3 beliebige Punkte handelt, ist anzunehmen, dass das Ergebnis genauso für alle anderen Punkte des Kreisbogens gelten wird.

Thales von Milet lebte etwa um 600 v. Chr. und war Mathematiker, Ingenieur, Astronom und Natuphilosoph. Da er ihn exakt beweisen konnte, wurde der Satz des Thales nach ihm benannt.

Schritt 1:

Wir konstruieren die Strecke 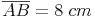$\overline{AB} = 8\ cm$ und beschriften die Eckpunkte.

Schritt 2:

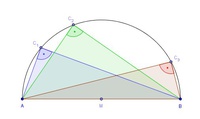
Halbieren Sie die Strecke 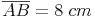$\overline{AB} = 8\ cm$ und benennen Sie den so erhaltenen Punkt als Mittelpunkt M.

Zeichnen Sie nun einen Kreisbogen über die Strecke 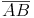$\overline{AB}$ . Stechen Sie dazu mit dem Zirkel im Punkt M ein, spannen Sie diesen entweder bis zum Punkt A oder B und zeichnen Sie den Bogen.

Schritt 3:

Wählen Sie drei beliebige Punkte auf dem Kreisbogen und beschriften Sie diese mit 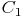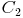C_1 , C_2 und C_3 .

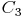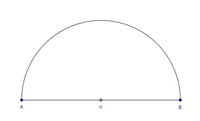
Schritt 4:

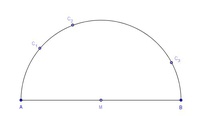
Verbinden Sie nun jeden dieser 3 Punkte mit den Punkten A und B.

Dabei entstehen drei Dreiecke. Durch Nachmessen können wir erkennen, dass es sich um drei rechtwinkelige Dreiecke handelt. Jeder der Punkte auf dem Kreisbogen schließt einen rechten Winkel ein.

Der Satz von Thales:

Jeder Winkel im Halbkreis ist ein rechter Winkel.

Dieser Artikel hat mir geholfen. das half mir
... leider nicht ... leider nicht
Kommentar Kommentar
4,2
146 Bewertungen

Kommentar #533 von Ubbo 13.12.11 16:54 Ubbo: super erklärt!
Kommentar #40328 von Mike 02.11.17 11:16 Mike: super! danke!
Kommentar #43328 von lol 15.12.19 18:02 lol: cool danke
Kommentar #43406 von kohf 08.01.20 15:56 kohf: Toll. Danke, Thales. :)

Satz von Thales

Der Satz von Thales

Kommentar verfassen