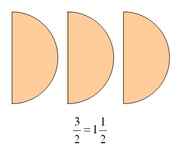Formelsammlung Brüche
Auf dieser Seite finden Sie die wichtigsten Erklärungen und Formeln rund um das Thema Bruchrechnung zusammengefasst. Möchten Sie genauere Informationen über die Erklärungen und Formeln, so wählen Sie bitte die entsprechenden Unterseiten im Menü aus.
Allgemeines:
Begriffe:
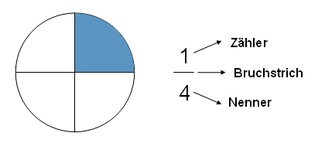
Ein Bruch besteht (von oben nach unten gelesen) aus Zähler, Bruchstrich und Nenner.
Ein Bruch besteht (von oben nach unten gelesen) aus Zähler, Bruchstrich und Nenner.
Brucharten:
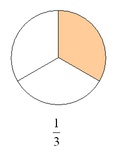
Echte Brüche:
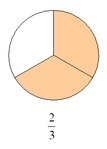
Bei echten Brüchen ist der Zähler kleiner als der Nenner.
Bei echten Brüchen ist der Zähler kleiner als der Nenner.
Unechte Brüche:
Bei unechten Brüchen ist der Zähler größer als der Nenner.
Bei unechten Brüchen ist der Zähler größer als der Nenner.
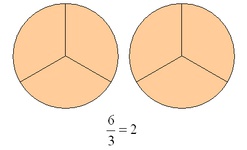
Uneigentliche Brüche:
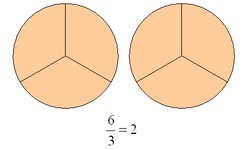
Bei uneigentlichen Brüchen ist der Zähler gleich groß wie der Nenner oder ein Vielfaches des Nenners.
Bei uneigentlichen Brüchen ist der Zähler gleich groß wie der Nenner oder ein Vielfaches des Nenners.
Stammbrüche:
Brüche, deren Zähler 1 ist, nennt man Stammbrüche.
Brüche, deren Zähler 1 ist, nennt man Stammbrüche.
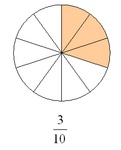
Dezimalbrüche:
Brüche, deren Nenner eine dekadische Einheit (10, 100, 1000, ...) sind, nennt man Dezimalbrüche.
Brüche, deren Nenner eine dekadische Einheit (10, 100, 1000, ...) sind, nennt man Dezimalbrüche.
Schreibweise von Brüchen
Der Bruch als Division:
Der Bruchstrich ist ein Divisionszeichen.
Ein Bruch bedeutet also Zähler dividiert durch Nenner.
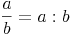
Der Bruchstrich ist ein Divisionszeichen.
Ein Bruch bedeutet also Zähler dividiert durch Nenner.
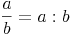
Ganze
Ganze bei uneigentlichen Brüchen:
Bei uneigentlichen Brüchen ist der Zähler gleich groß wie der Nenner oder ein Vielfaches des Nenners.
Der Wert eines uneigentlichen Bruches ist also immer eine ganze Zahl.
Bei uneigentlichen Brüchen ist der Zähler gleich groß wie der Nenner oder ein Vielfaches des Nenners.
Der Wert eines uneigentlichen Bruches ist also immer eine ganze Zahl.
Eine gemischte Zahl in einen unechten Bruch umwandeln:
Zähler: Multiplizieren Sie die ganze Zahl mit dem Nenner und addieren Sie den Zähler.
Nenner: diesen können Sie abschreiben.
z.B.: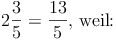
Zähler: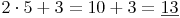
Nenner: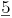
Zähler: Multiplizieren Sie die ganze Zahl mit dem Nenner und addieren Sie den Zähler.
Nenner: diesen können Sie abschreiben.
z.B.:
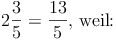
Zähler:
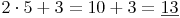
Nenner:
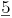
Einen unechten Bruch in eine gemischte Zahl umwandeln:
Dividieren Sie den Zähler durch den Nenner. Das ganzzahlige Ergebnis gibt die Anzahl der Ganzen an. Der Rest gibt den Zähler des Restbruches an.
z.B.: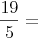
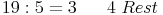
Zusammenfassung: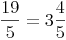
Dividieren Sie den Zähler durch den Nenner. Das ganzzahlige Ergebnis gibt die Anzahl der Ganzen an. Der Rest gibt den Zähler des Restbruches an.
z.B.:
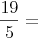
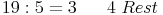
Zusammenfassung:
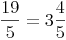
Erweitern und kürzen
Erweitern eines Bruches:
Der Wert eines Bruches bleibt gleich, wenn man Zähler und Nenner mit derselben Zahl multipliziert.
z.B. mit 3 erweitert ergibt
mit 3 erweitert ergibt  .
.
Der Wert eines Bruches bleibt gleich, wenn man Zähler und Nenner mit derselben Zahl multipliziert.
z.B.
 mit 3 erweitert ergibt
mit 3 erweitert ergibt  .
.
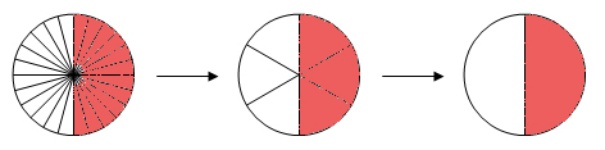
Kürzen eines Bruches:
Der Wert eines Bruches bleibt gleich, wenn man Zähler und Nenner durch dieselbe Zahl dividiert.
z.B. durch 3 dividiert (= gekürzt) ergibt
durch 3 dividiert (= gekürzt) ergibt  .
.
Der Wert eines Bruches bleibt gleich, wenn man Zähler und Nenner durch dieselbe Zahl dividiert.
z.B.
 durch 3 dividiert (= gekürzt) ergibt
durch 3 dividiert (= gekürzt) ergibt  .
.
Bruchteile von Größen
Bruchteile von Größen:
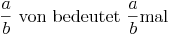
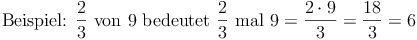
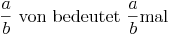
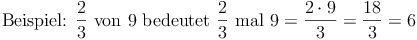
Umkehraufgaben: Das Ganze berechnen:
Kennt man nur einen Bruchteil der Gesamtgröße und dessen Wert, so dividiert man den Wert zuerst durch den Zähler und multipliziert ihn anschließend mit dem Nenner, um die Gesamtgröße zu erhalten.
Beispiel: einer Strecke sind 210km:
einer Strecke sind 210km: 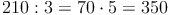 km.
km.
Kennt man nur einen Bruchteil der Gesamtgröße und dessen Wert, so dividiert man den Wert zuerst durch den Zähler und multipliziert ihn anschließend mit dem Nenner, um die Gesamtgröße zu erhalten.
Beispiel:
 einer Strecke sind 210km:
einer Strecke sind 210km: 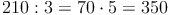 km.
km.
Umkehraufgaben: Bruchteile berechnen:
Kennt man den Gesamtwert und den Wert eines Teiles und möchte den Bruchteil dieses Teiles berechnen, so bildet man folgenden Bruch:
Den Wert eines Teiles schreibt man in den Zähler, den Gesamtwert schreibt man in den Nenner.
Beispiel: 4 von 15 Kindern haben blonde Haare: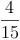
Kennt man den Gesamtwert und den Wert eines Teiles und möchte den Bruchteil dieses Teiles berechnen, so bildet man folgenden Bruch:
Den Wert eines Teiles schreibt man in den Zähler, den Gesamtwert schreibt man in den Nenner.
Beispiel: 4 von 15 Kindern haben blonde Haare:
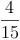
Dezimalzahlen in Brüche umwandeln
Dezimalzahlen mit endlich vielen Dezimalstellen in Brüche umwandeln:
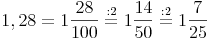
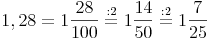
Dezimalzahlen mit periodischen Dezimalstellen in Brüche umwandeln:
Die periodische Ziffer wird in den Zähler geschrieben. Im Nenner schreibt man die Ziffer 9 so oft, wie es periodische Ziffern gibt.
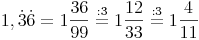
Die periodische Ziffer wird in den Zähler geschrieben. Im Nenner schreibt man die Ziffer 9 so oft, wie es periodische Ziffern gibt.
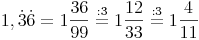
Gemischt periodische Dezimalzahlen in Brüche umwandeln:
(bei einer Dezimalzahl mit 2 Dezimalstellen, wobei die letzte davon periodisch ist)
1) Den Wert für 100x berechnen
2) Den Wert für 10x berechnen
3) Die beiden entstandenen Gleichungen subtrahieren
4) Den Wert für 1x ausdrücken (durch dividieren)
Beispiel: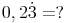
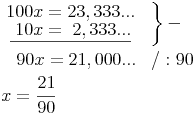
(bei einer Dezimalzahl mit 2 Dezimalstellen, wobei die letzte davon periodisch ist)
1) Den Wert für 100x berechnen
2) Den Wert für 10x berechnen
3) Die beiden entstandenen Gleichungen subtrahieren
4) Den Wert für 1x ausdrücken (durch dividieren)
Beispiel:
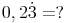
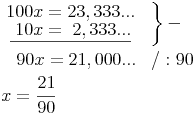
Brüche in Dezimalzahlen umwandeln
Das Ergebnis ist eine Dezimalzahl mit endlich vielen Dezimalstellen:
Ein Bruch kann durch Dividieren in eine Dezimalzahl umgewandelt werden. Der Bruchstrich fungiert dabei als Divisionszeichen.
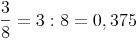
Ein Bruch kann durch Dividieren in eine Dezimalzahl umgewandelt werden. Der Bruchstrich fungiert dabei als Divisionszeichen.
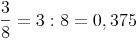
Das Ergebnis ist eine periodische Dezimalzahl:
Ein Bruch kann durch Dividieren in eine Dezimalzahl umgewandelt werden.
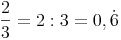
Der Bruchstrich fungiert dabei als Divisionszeichen.
Ein Bruch kann durch Dividieren in eine Dezimalzahl umgewandelt werden.
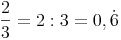
Der Bruchstrich fungiert dabei als Divisionszeichen.
Das Ergebnis ist eine gemischt periodische Dezimalzahl:
Ein Bruch kann durch Dividieren in eine Dezimalzahl umgewandelt werden.
Der Bruchstrich fungiert dabei als Divisionszeichen.
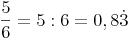
Ein Bruch kann durch Dividieren in eine Dezimalzahl umgewandelt werden.
Der Bruchstrich fungiert dabei als Divisionszeichen.
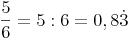
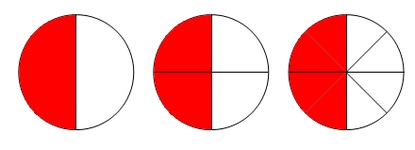
Brüche auf dem Zahlenstrahl
Um einen Bruch auf dem Zahlenstrahl darstellen zu können, dividiert man Zähler durch Nenner.
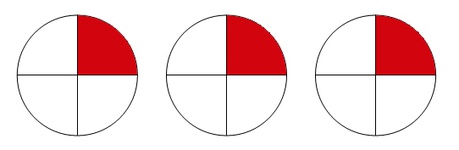
Verschiedene Brüche, die denselben Wert haben, stellen auf dem Zahlenstrahl denselben Punkt dar.
Beispiel: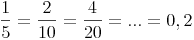
Verschiedene Brüche, die denselben Wert haben, stellen auf dem Zahlenstrahl denselben Punkt dar.
Beispiel:
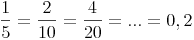
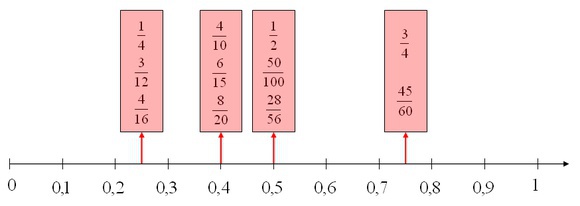
Brüche vergleichen
Brüche gleichnamig machen:
Gleichnamig machen bedeutet, dass man die Brüche auf denselben Nenner bringt.
Hat man Brüche gleichnamig gemacht (auf den gleichen Nenner gebracht), so ist jener Bruch größer, der den größeren Zähler hat.
Gleichnamig machen bedeutet, dass man die Brüche auf denselben Nenner bringt.
Hat man Brüche gleichnamig gemacht (auf den gleichen Nenner gebracht), so ist jener Bruch größer, der den größeren Zähler hat.
Man kann Brüche miteinander vergleichen, indem man sie in Dezimalzahlen umwandelt.
z.B.:
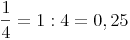 .
.
Addieren und subtrahieren von Brüchen
Addieren und subtrahieren mit gleichnamigen Brüchen:
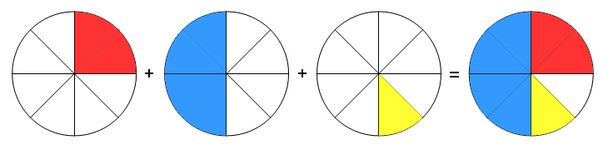
Beim Addieren und Subtrahieren gleichnamiger Brüche werden die Zähler addiert (subtrahiert) und die Nenner unverändert gelassen.
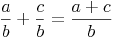
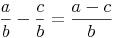
Beim Addieren und Subtrahieren gleichnamiger Brüche werden die Zähler addiert (subtrahiert) und die Nenner unverändert gelassen.
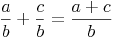
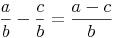
Addieren und subtrahieren mit ungleichnamigen Brüchen:
Beim Addieren und Subtrahieren gleichnamiger Brüche werden die Zähler addiert (subtrahiert) und die Nenner unverändert gelassen.
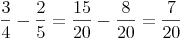
Beim Addieren und Subtrahieren gleichnamiger Brüche werden die Zähler addiert (subtrahiert) und die Nenner unverändert gelassen.
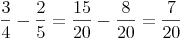
Multiplizieren von Brüchen
Multiplikation eines Bruches mit einer Zahl:
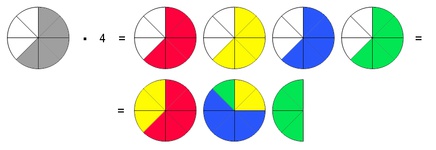
Man multipliziert einen Bruch mit einer Zahl, indem man die Zahl mit dem Zähler multipliziert und den Nenner unverändert lässt.
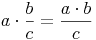
Man multipliziert einen Bruch mit einer Zahl, indem man die Zahl mit dem Zähler multipliziert und den Nenner unverändert lässt.
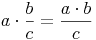
Multiplizieren von Brüchen:
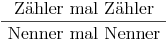
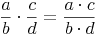
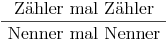
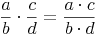
Dividieren von Brüchen
Division eines Bruches durch eine Zahl:
Der Zähler wird unverändert gelassen, der Nenner wird mit der natürlichen Zahl multipliziert!
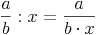
Beispiel: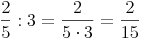
Der Zähler wird unverändert gelassen, der Nenner wird mit der natürlichen Zahl multipliziert!
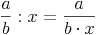
Beispiel:
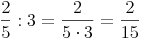
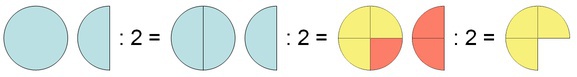
Man dividiert einen Bruch durch einen anderen Bruch, indem man den 1. Bruch mit dem Kehrwert des 2. Bruches multipliziert.
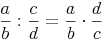
Beispiel: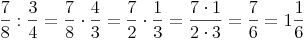
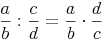
Beispiel:
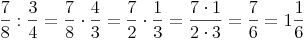
Verbindung der 4 Grundrechnungsarten (Vorrangregeln)
Auch beim Rechnen mit Brüchen gelten folgende Vorrangregeln:
1. Klammern auflösen (Reihenfolge: runde, eckige, geschwungene, Klammern)
2. Punktrechnungen ausführen ( , :)
, :)
3. Strichrechnungen ausführen (+, -)
Wichtig: Auch innerhalb einer Klammer gilt: Punkt vor Strich!
1. Klammern auflösen (Reihenfolge: runde, eckige, geschwungene, Klammern)
2. Punktrechnungen ausführen (
 , :)
, :)3. Strichrechnungen ausführen (+, -)
Wichtig: Auch innerhalb einer Klammer gilt: Punkt vor Strich!
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar