Das Volumen des dreiseitigen Prismas
Um das Volumen eines Prismas zu berechnen, berechnet man zuerst den Flächeninhalt der Grundfläche.
Diese Flächen werden dann h Mal (h = Höhe) übereinander gelegt, sodass es Prisma entsteht.
Für die Volumsberechnung gilt also allgemein: Grundfläche mal Höhe, wobei es sich in unserem Fall bei der Grundfläche um ein Dreieck handelt.
Grundfläche = rechtwinkeliges Dreieck:
Flächeninhalt eines rechtwinkeligen Dreiecks:
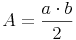
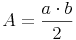
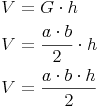
Flächeninhalt eines gleichseitigen Dreiecks:
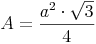
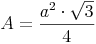
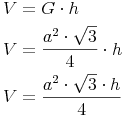
Flächeninhalt eines allgemeinen Dreiecks:
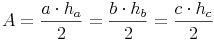
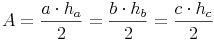
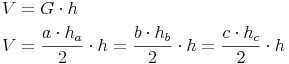
Das Volumen eines dreiseitigen Prismas:
Volumen = Grundfläche mal Höhe
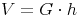
Volumen = Grundfläche mal Höhe
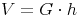
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Aldwin
Die seite hat mir viel geholfen und ich werde sie weiterempfehlen an meine klasse, danke für die hilfreichen Formeln 9aM
JG
Die Seite hat mir bisschen mehr geholfen als die anderen aber trotzdem weiss ich noch nicht wie die Formel zur Berechnung des Volumens heisst!
james
DIE SEITE HAT MIR MEGA GEHOLFEN BESSER ALS MEINE MATHE LEHRERIN ES ERKLÄREN KONNTE DAS THEMA IST SOGAR EINFACHER ALS ICH DACHTE DANKE
pji
Es hilft mega. :)
machmal versteht man es doch nicht. aber hilft