Rechtssystem
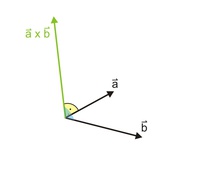
Die Vektoren a, b und das Kreuzprodukt a x b bilden ein sogenanntes Rechtssystem. Um sich dies besser vorzustellen, kann man die ersten drei Finger der rechten Hand zur Hilfe nehmen, wobei man Daumen, Zeigefinger und Mittelfinger so voneinander abspreizt, dass alle normal zueinander stehen.
- Wenn Vektor a in Richtung Daumen zeigt
- und Vektor b in Richtung Zeigefinger,
- dann zeigt das Kreuzprodukt (a x b) in Richtung des Mittelfingers
- der rechten Hand!
Weitere Informationen dazu kann man bei Wikipedia (Rechtssystem) nachlesen:
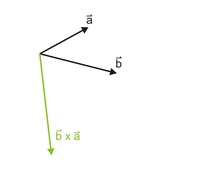
Vertauscht man die beiden Vektoren und bildet das Kreuzprodukt (b x a), so kann man folgende Zusammenhänge feststellen:
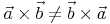
Weiters gilt:
- Die Beträge der beiden Kreuzprodukte sind gleich
- Die Richtung der beiden Kreuzprodukte sind gleich
- Die Orientierung der beiden Kreuzprodukte sind unterschiedlich
Kommutativgesetz
Auf das vektorielle Produkt kann nicht das Kommutativgesetz (Vertauschungsgesetz) angewendet werden. Ein Beispiel zur Veranschaulichung:
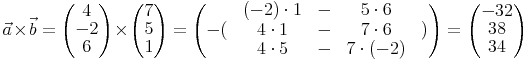
Einige weiterführende Überlegungen:
Das Kreuzprodukt steht normal zu den beiden Vektoren
Die Gültigkeit für dieses Beispiel (Hinweis: dies gilt nicht als Beweis) kann man zeigen, indem man das skalare Produkt mit den beiden Vektoren bildet. Das skalare Produkt von zwei normal zueinander stehenden Vektoren müsste ja 0 ergeben:
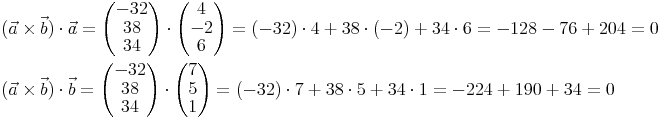
Fläche des Parallelogramms
Der Betrag des Kreuzprodukts ergibt die Fläche des Parallelogramms, das die beiden Vektoren a, b aufspannen:
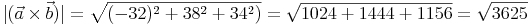
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar