Differenzenregel

Die Differenzenregel ist der logische Umkehrschluss zur Summenregel

Differenzenregel

Die Differenzenregel ist das Komplementär zur Summenregel. Nicht nur Differentiale von summierten Funktionen können zerlegt werden, auch bei Differenzen von Summen ist dies möglich

Differenzenregel

Gegeben seien die beiden differenzierbaren Funktionen f₁, f₂ und g mit

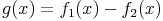
Somit ist auch g differenzierbar und es gilt:

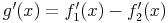
Die Ableitung einer Differenz ist somit die Differenz der einzelnen Ableitungen (von Minuend und Subtrahend).

Erklärung

Mit Hilfe der Summenregel und der Konstantenregel lässt sich die Differenzenregel erklären. Laut Summenregel gilt für

$\begin{align} & g(x)=f_1(x)+f_2(x) \\ & g'(x)=f_1'(x)+f_2'(x) \\ \end{align}$

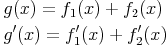
Ist nun

$f_2(x)=(-1) \cdot h(x)$

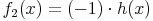
so gilt dank Konstantenregel:

$f_2'(x)=(-1) \cdot h'(x)$

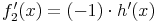
Nach Substituieren von f_2' erhält man:

g'(x)=f_1'(x)+(-1)h'(x)=f_1'(x)-h'(x)

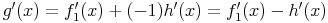
Beispiele zur Differenzenregel

Beispiel 1:

$\begin{align} & f(x)=7x^2-4x \\ & f'(x)=\left(7x^2-4x\right)'=\left(7x^2\right)'-\left(4x\right)'=14x-4 \\ \end{align}$

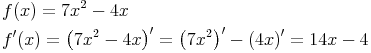
Beispiel 2:

$\begin{align} & f(x)=2x^4-5x^3+7x^2-11x+2 \\ & f'(x)=\left(2x^4-5x^3+7x^2-11x+2\right)' \\ & f'(x)=\left(2x^4\right)'-\left(5x^3\right)'+\left(7x^2\right)'-\left(11x\right)'+\left(2\right)' \\ & f'(x)=8x^3-15x^2+14x-11+0 \\ \end{align}$

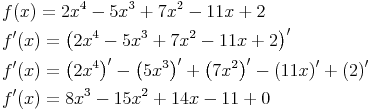
Anmerkung: Bei beiden Beispielen kam die Potenzfunktion als Ableitungsfunktion und beim zweiten Beispiel auch die Summenregel zur Anwendung.

Dieser Artikel hat mir geholfen. das half mir
... leider nicht ... leider nicht
Kommentar Kommentar
2,5
11 Bewertungen

Differenzenregel