Summenregel

Durch die Summenregel können summierte Funktionen in "übersichtlichere Portionen" aufgeteilt werden

Summenregel

Die Summenregel ermöglicht es sehr leicht summierte Funktionen in einfachere Konstrukte zu zerlegen.

Summenregel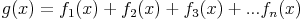

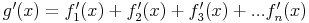
Gegeben seien beliebig viele differenzierbare Funktionen f1, f2, f3, ... fn und g mit

g(x)=f_1(x) + f_2(x) + f_3(x) + ... f_n(x)

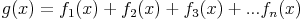
Somit ist auch g differenzierbar und es gilt:

g'(x)=f_1'(x)+f_2'(x)+f_3'(x)+...f_n'(x)

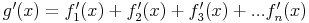
Die Ableitung einer Summe ist somit die Summe der einzelnen Ableitungen.

Beispiele zur Summenregel

Beispiel 1:

\begin{align} & f(x)=3x^2+5x \\ & f'(x)=\left(3x^2+5x\right)'=\left(3x^2\right)'+\left(5x\right)'=6x+5 \\ \end{align}

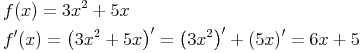
Beispiel 2:

\begin{align} & f(x)=2x^4-5x^3+7x^2-11x+2 \\ & f'(x)=\left(2x^4-5x^3+7x^2-11x+2\right)' \\ & f'(x)=\left(2x^4\right)'-\left(5x^3\right)'+\left(7x^2\right)'-\left(11x\right)'+\left(2\right)' \\ & f'(x)=8x^3-15x^2+14x-11+0 \\ \end{align}

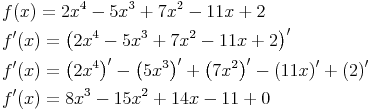
Anmerkung: Bei beiden Beispielen kam die Potenzfunktion als Ableitungsfunktion und beim zweiten Beispiel auch die Differenzenregel zur Anwendung.

Kommentar #7760 von me 09.06.13 15:39
me

Ein beweis wäre noch schön anzusehen

Kommentar verfassen