Extremstellen von rationalen Funktionen ermitteln

In diesen Beispielen werden die Extremstellen von rationalen Funktionen ermittelt und dabei auf deren Besonderheiten eingegangen.

Auf dieser Seite ermitteln wir die Extremstellen (Hochpunkte, Tiefpunkte, Sattelpunkte) von gebrochen rationalen Funktionen und gehen dabei nach den Teilschritten vor, die wir im Detail bei den allgemeinen Erklärungen zur Ermittlung von Extremstellen ausgeführt haben.

Beispiel: Einfache rationale Funktion

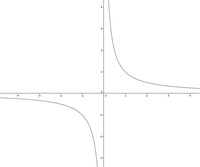
Wir beginnen mit der einfachsten rationalen Funktion:

f(x) = \frac{1}{x}
Rationale Funktion, keine Extremstellen Beispiel 1

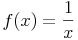
Weiters bilden wir wieder die ersten beiden Ableitungen:

\begin{align} f(x) & = \frac{1}{x} = x^-1 \\ f'(x) & = (-1) \cdot x^{-2} = -x^{-2} && \text{oder}\ -\frac{1}{x^2} \\ f''(x) & = (-2) \cdot (-x^{-3}) = 2x^{-3} && \text{oder}\ -\frac{2}{x^3} \\ \end{align}

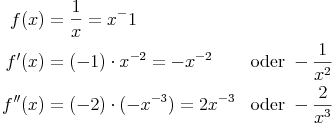
1. Extremstellen ermitteln

\begin{align} f'(x) & = -\frac{1}{x^2} \\ f'(x) & = 0 \\ -\frac{1}{x^2} & = 0 \\ & && \rightarrow \text{Gleichung nicht lösbar} \\ \end{align}

Da die Gleichung nicht lösbar ist, besitzt diese Funktion keine Extremstellen. Man erkennt, dass sich die Funktion zwar gegen Null tendiert, wenn man unendlich weit nach links oder nach rechts wandert, die Funktionswerte werden aber dennoch immer größer oder kleiner Null sein (und niemals exakt Null).
Anmerkung: Schritt 2 und 3 sind hier somit nicht notwendig

Beispiel: Rationale Funktion mit zwei Extremstellen

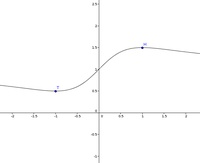
Nun wenden wir uns einer Funktion zu, die auch tatsächlich Extremstellen besitzt. In diesem Fall sin ddie Ableitungen nicht ganz trivial und es ist die Kenntnis einiger Ableitungsregeln erforderlich.

  • Quotientenregel
    Sowohl für die erste als auch für die zweite Ableitung ist die Quotientenregel erforderlich, das bedeutet Zähler und Nenner eines Bruchs werden in zwei Teilfunktionen gesplittet. Diese Teilfunktionen führen wir der Vollständigkeit halber immer separat und setzen diese dann in die endgültige Gleichung ein.
  • Kettenregel
    Bei der zweiten Ableitung ist auch noch die Kettenregel erforderlich (und zwar bei der Ableitung der zweiten Teilfunktion).
\begin{align} f(x) = \frac{x^2 + x + 1}{1 + x^2} \\ \end{align}
Rationale Funktion, zwei Extremstellen Beispiel 2

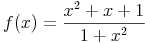
Wir bilden nun die ersten beiden Ableitungen. Zuerst f'(x):

\begin{align} f(x) & = \frac{x^2 + x + 1}{1 + x^2} = \frac{f_1(x)}{f_2(x)} \\ & \\ f_1(x) & = x^2 + x + 1 \\ f_1'(x) & = 2x + 1 \\ f_2(x) & = 1 + x^2 \\ f_2'(x) & = 2x \\ & \\ f'(x) & = \frac{f_1'(x) \cdot f_2(x) - f_1(x) \cdot f_2'(x)}{(f_2(x))^2} && \rightarrow \text{Quotientenregel} \\ f'(x) & = \frac{(2x + 1) \cdot (1 + x^2) - (x^2 + x + 1) \cdot 2x}{(1 + x^2)^2} = \\ & = \frac{2x + 1 + 2x^3 + x^2 - 2x^3 - 2x^2 - 2x}{(1 + x^2)^2} = \\ & = \frac{1 - x^2}{(1 + x^2)^2} \\ \end{align}

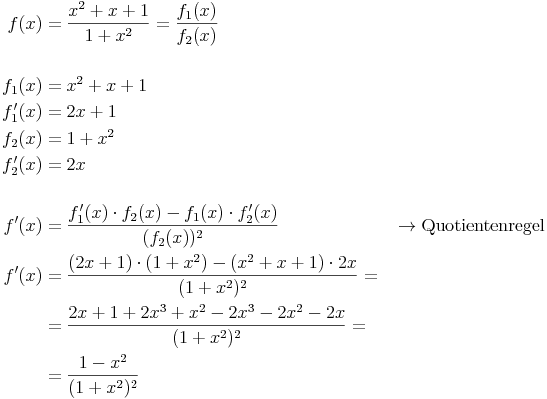
Die zweite Ableitung f''(x) bilden wir ebenfalls mit Hilfe der Quotientenregel, indem wir f'(x) erneut in zwei Teilfunktionen aufsplitten:

\begin{align} f'(x) & = \frac{1 - x^2}{(1 + x^2)^2} = \frac{f_1(x)}{f_2(x)} \\ & \\ f_1(x) & = 1 - x^2 \\ f_1'(x) & = -2x \\ f_2(x) & = (1 + x^2)^2 \\ f_2'(x) & = 2 \cdot (1 + x^2) \cdot 2x = 4x \cdot (1 + x^2) && \rightarrow \text{Kettenregel} \\ & \\ f''(x) & = \frac{f_1'(x) \cdot f_2(x) - f_1(x) \cdot f_2'(x)}{(f_2(x))^2} && \rightarrow \text{Quotientenregel} \\ f''(x) & = \frac{-2x \cdot (1 + x^2)^2 - (1-x^2) \cdot 4x (1 + x^2)}{(1 + x^2)^4} = \\ & = \frac{(1 + x^2) [-2x (1 + x^2) - 4x (1 - x^2)]}{(1 + x^2)^4} = \\ & = \frac{-2x (1 + x^2) - 4x (1 - x^2)}{(1 + x^2)^3} = \\ & = \frac{-2x [(1 + x^2) - 2 (1 - x^2)]}{(1 + x^2)^3} = \\ & = \frac{-2x (1 + x^2 + 2 - 2x^2)}{(1 + x^2)^3} = \\ & = \frac{-2x (3 - x^2)}{(1 + x^2)^3} \\ \end{align}

1. Extremstellen ermitteln
Die rationale Funktion f'(x) kann nur den Wert 0 erlangen, wenn der Zähler 0 wird. Der Nenner kann somit ignoriert werden und die Gleichung wird mit einem Schlag einfacher. Einzig der Wertebereich der Funktion muss hier berücksichtigt werden und - wie bei jeder anderen Funktion ermittelt werden:

\begin{align} & \text{1a. Definitionsbereich ermitteln:} \\ (1 + x^2)^2 & = 0 && / \sqrt{\ } \\ 1 + x^2 & = 0 && / -1 \\ x^2 & = -1 && / \sqrt{\ } \\ x & = \sqrt{-1} && \rightarrow \text{im reellen Zahlenraum nicht lösbar} \\ & && \rightarrow \text{alle reellen Zahlen möglich} \\ & \\ & \text{1b. Extremstellen ermitteln:} \\ 1 - x^2 & = 0 && / -1 \\ - x^2 & = -1 && / \cdot (-1) \\ x^2 & = 1 && / \sqrt{\ } \\ x_{1,2} & = \pm 1 \\ \end{align}

2. Art der Extremstellen ermitteln

\begin{align} f''(1) & = \frac{-2 \cdot 1 \cdot (3 - 1^2)}{(1 + 1^2)^3} = \frac{-2 \cdot 2}{2^3} = \frac{-4}{8} = -0.5 < 0 && \rightarrow \text{Hochpunkt} \\ & \\ f''(-1) & = \frac{-2 \cdot (-1) \cdot (3 - (-1)^2)}{(1 + (-1)^2)^3} = \frac{2 \cdot 2}{2^3} = \frac{4}{8} = 0.5 > 0 && \rightarrow \text{Tiefpunkt} \\ \end{align}

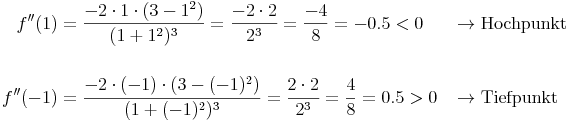
3. Funktionswerte ermitteln

\begin{align} f(1) & = \frac{1^2 + 1 + 1}{1 + 1^2} = \frac{3}{2} \\ & \\ f(-1) & = \frac{(-1)^2 + (-1) + 1}{1 + (-1)^2} = \frac{1}{2} \\ \end{align}

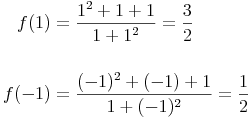
Die Funktion besitzt somit einen Hochpunkt an der Stelle H(1, 1.5) und einen Tiefpunkt an der Stelle T(-1, 0.5)

Kommentar verfassen