Höhere Ableitungen

Höhere Ableitungen sind speziell für Kurvendiskussionen und praktische Anwendungsfälle wie in der Physik erforderlich.

Begriffsbildung

Was versteht man unter einer höheren Ableitung? Dies ist an sich recht simpel: Wird die Ableitung einer Funktion (f) gebildet, so ergibt das Ergebnis wieder eine Funktion (f'). Diese Funktion kann natürlich nach den gleichen Rechenregeln der Differentialrechnung erneut abgeleitet werden. Man spricht dann von der zweiten Ableitung (f'') von der Funktion (f). Wiederholt man den Schritt erneut, erhält man die dritte Ableitung (f'''), usw.

Beispiel

Anhand eines konkreten Beispiels wird der Sachverhalt klarer:

f(x) = - x^4 + 3 \cdot x^3 - 5 \cdot x^2 +2 \cdot x - 1

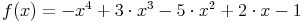
Die erste Ableitung dieser Funktion lautet:

f'(x) = - 4 \cdot x^3 + 9 \cdot x^2 - 10 \cdot x + 2

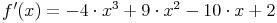
Diese neue Funktion wird nun erneut abgeleitet. Die weiteren Ableitungen (2., 3., 4.) lauten somit:

\begin{align} f''(x) &= - 12 \cdot x^2 + 18 \cdot x - 10 \\ f'''(x) & = - 24 \cdot x + 18 \\ f''''(x) & = -24 \\ \end{align}

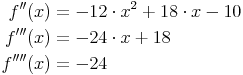
Für die Kurvendiskussion sind im Regelfall die ersten drei Ableitungen der Ausgangsfunktion erforderlich.

Höhere Ableitungen in der Physik

Vor allem in den technischen Bereichen sind höhere Ableitungen durchaus die Regel. Deswegen möchten wir auch noch ein etwas Realitäts-näheres Beispiel anführen: In der Mechanik kennt man die physikalischen Größen Beschleunigung, Geschwindigkeit und zurückgelegter Weg . Diese drei Größen charakterisieren das Bewegungsprofil eines Objektes und hängen bei genauerer Betrachtung von einander ab. Der Einfachheit halber gehen wir von einer gleichmäßig beschleunigten Bewegung aus.

In diesem Fall ist die Beschleunigung immer gleich, d.h. die Beschleunigung kann als konstante Funktion abgebildet werden:

a(t) = 2 m/s^2

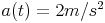
Die Beschleunigung gibt an, um wie viel sich die Geschwindigkeit in einer bestimmten Zeiteinheit ändert. Wenn die Beschleunigung konstant ist, bedeutet dies, dass die Geschwindigkeit in gleichen Abständen immer um den gleichen Betrag zunimmt / abnimmt. Daraus ergibt sich eine lineare Funktion für die Berechnung der Geschwindigkeit:

v(t) = a \cdot t = 2 \cdot t

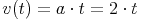
Wenn von Sekunde zu Sekunde die Geschwindigkeit um ein konstantes Maß zunimmt, muss die Differenz des zurück gelegten Weges immer höher werden:

s(t) = \frac{a}{2} \cdot t^2

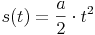
Stellt man die Formeln nun in umgekehrter Reihenfolge gegenüber, erkennt man folgenden Zusammenhang:

\begin{align} s(t) & = \frac{a}{2} \cdot t^2 \\ v(t) = s'(t) & = \frac{2 \cdot a}{2} \cdot t = a \cdot t \\ a(t) = s''(t) & = a \\ \end{align}

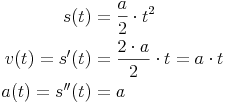
  • Die erste Ableitung der Weg-Funktion s'(t) ist die Geschwindigkeit-Funktion v(t)
  • Die zweite Ableitung der Weg-Funktion s''(t) ist die Beschleunigung-Funktion a(t)

Kommentar verfassen