Vergrößern von Figuren 1
Vergrößern von Figuren 2
Vergrößern von Figuren 3
Vergrößern von Figuren 4Auf dieser Seite zeigen wir Ihnen, wie Sie mit Hilfe der zentrischen Streckung Figuren vergrößern können.
Der Streckungsfaktor wird mit k bezeichnet. Ist k >1, so werden Figuren vergrößert. (bei k=2 um das Doppelte, bei k=3 um das Dreifache, ...)
Beispiel:
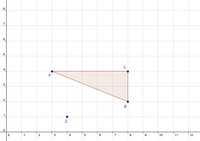
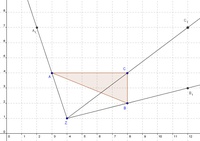
Konstruieren Sie das Dreieck ABC mit den Koordinaten A (3 / 4), B (8 / 2) und C (8 / 4).
Vergrößern Sie nun dieses Dreieck um den Streckungsfaktor k = 2 vom Streckungszentrum Z (4 / 1) aus.
Schritt 1:
Zeichen Sie die Punkte A, B und C in einem rechtwinkeligen Koordinatensystem ein und verbinden Sie diese zu einem Dreieck.
Konstruieren Sie in diesem Schritt auch gleich das Streckungszentrum Z.
Schritt 2:
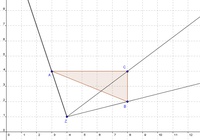
Zeichnen Sie nun drei Strahlen vom Streckungszentrum Z aus durch die Eckpunkte des Dreiecks.
Schritt 3:
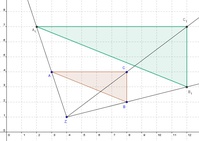
Nachdem der Streckungsfaktor k = 2 beträgt, müssen die Abstände vom Streckungszentrum Z zu den Eckpunkten A, B und C verdoppelt werden.
Stechen Sie dazu mit dem Zirkel im Punkt Z ein und spannen Sie bis zum Punkt A. Belassen Sie diesen Abstand im Zirkel, stechen nun im Eckpunkt A ein und schlagen diesen Abstand auf dem entsprechenden Strahl ab. Dadurch haben Sie nun den Eckpunkt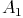 
konstruiert.
Wiederholen Sie diesen Vorgang auch für die Punkte B und C,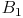 
und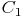 
zu erhalten.
Schritt 4:
Verbinden Sie die Punkte 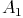, 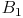und 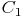miteinander, um das vergrößerte Dreieck zu erhalten.
Lösungen: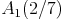
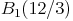
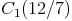
Figuren können durch die zentrische Streckung vergrößert werden. Dazu muss der Streckungsfaktor k größer als 1 sein.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Ich
Echt schlecht erklärt
Hans
Ich hab gar nichts verstanden aber vielleicht ligt es auch einfach an meinem hohen IQ