Verkleinern 1
Verkleinern 2
Verkleinern 3
Verkleinern 4Auf dieser Seite zeigen wir Ihnen, wie Sie mit Hilfe der zentrischen Streckung Figuren verkleinern können.
Der Streckungsfaktor wird mit k bezeichnet. Gilt 0 < k < 1, so werden Figuren verkleinert. (bei k=0,5 auf die Hälfte, bei k=0,25 auf ein Viertel, ...)
Beispiel:
Konstruieren Sie das Dreieck ABC mit den Koordinaten A (1 / 10), B (12 / 3) und C (12 / 9).
Verkleinern Sie nun dieses Dreieck um den Streckungsfaktor k = 0,5 vom Streckungszentrum Z (4 / 1) aus.
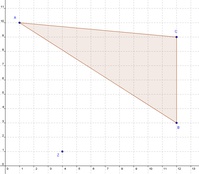
Schritt 1:
Zeichen Sie die Punkte A, B und C in einem rechtwinkeligen Koordinatensystem ein und verbinden Sie diese zu einem Dreieck.
Konstruieren Sie in diesem Schritt auch gleich das Streckungszentrum Z.
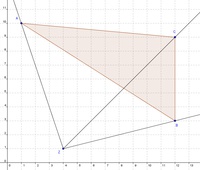
Schritt 2:
Zeichnen Sie nun drei Strahlen vom Streckungszentrum Z aus durch die Eckpunkte des Dreiecks.
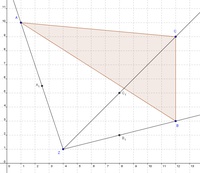
Schritt 3:
Nachdem der Streckungsfaktor k = 0,5 beträgt, müssen die Abstände vom Streckungszentrum Z zu den Eckpunkten A, B und C halbiert werden.
Lösen Sie dies rechnerisch, indem Sie die Abstände von Z bis A, B und C mit Hilfe des Geodreiecks abmessen und dann mit 0,5 multiplizieren. Da es sich in diesem besonderen Fall um Halbierungen handelt, können Sie diese spezielle Aufgabe auch geometrisch lösen, indem Sie die Streckensymmetralen der Strecken ZA, ZB und ZC konstruieren, um die Halbierungspunkte dieser Strecken zu erhalten.
So erhalten Sie die Punkte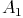 
, 
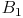und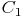 
des verkleinerten Dreiecks.
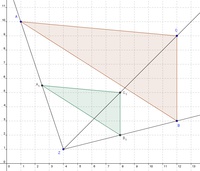
Schritt 4:>
Verbinden Sie die Punkte 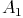, 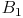und 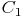, um das verkleinerte Dreieck zu erhalten.
Lösungen:
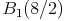
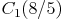
Figuren können durch zentrische Streckung verkleinert werden. Dazu muss der Streckungsfaktor k zwischen 0 und 1 liegen.
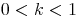
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar