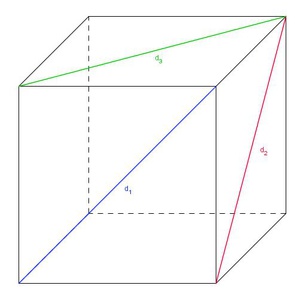
Die Flächendiagonale(n) eines Würfels
Eine Diagonale verbindet zwei gegenüberliegende Eckpunkte eines Quadrates.
Die Oberfläche eines Würfels besteht aus 6 gleich großen Quadraten.
Daher sind die Diagonalen aller 6 Seitenflächen eines Würfels gleich lang.
Es gilt: 
Die Flächendiagonale eines Würfels wird daher mit d bezeichnet.
Berechnung der Flächendiagonale eines Würfels
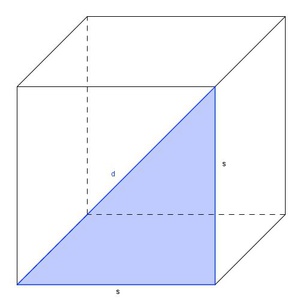
Zeichnet man die Flächendiagonale auf einer beliebigen Seitenfläche des Würfels ein, so teilt sie die Seitenfläche in zwei gleich große rechtwinkelige Dreiecke.
In jedem rechtwinkeligen Dreieck gilt der Lehrsatzes des Pythagoras, somit kann man mit dessen Hilfe die Länge der Flächendiagonale berechnen.
Die Flächendiagonale (d) ist die Hypotenuse (=längste Seite) des rechtwinkeligen Dreiecks, die beiden Kanten (s) sind die Katheten (= kürzeren Seiten). Daher gilt:
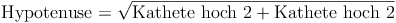
Wir setzen nun die Bezeichnungen in die Formel ein: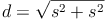
Nun kann noch addiert werden: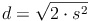
Partielles (=teilweises) Wurzelziehen: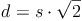
In einem Würfel sind alle Seiten gleich große Quadrate, daher sind auch alle Flächendiagonalen gleich lang und werden mit d bezeichnet.
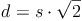
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Its a mystery
Kommt bei der Flächendiagonale und der Raumdiagonale hoch 2 herraus?
trol
Wie kann ich die Raumdiagonale in eine Flächendiagonale umrechnen?
L.R
Wie kann ich bei einem Würfel die Flächendiagonale ausrechnen, wenn ich nur die Raumdiagonale angegeben habe?
dimitri
Bei der Flächendiagonale im Würfel kann man doch einfach die Fläche des Quadrates durch 2 rechnen