Raumdiagonale eines Würfels

Die Raumdiagonale(n) des Würfels

Eine Raumdiagonale verbindet jeden Eckpunkt der Grundfläche (A, B, C, D) mit dem am weitest entfernten (= gegenüberliegenden) Eckpunkt der Deckfläche (E, F, G, H):

$\overline{AG}\ , \overline{BH}\ , \overline{CE}\ , \overline{DF}$

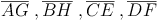
Die Oberfläche eines Würfels besteht aus 6 gleich großen Quadraten.

Daher sind auch die Raumdiagonalen eines Würfels gleich lang.

Die Raumdiagonale eines Würfels wird daher einheitlich mit 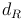bezeichnet.

Berechnung der Raumdiagonale eines Würfels

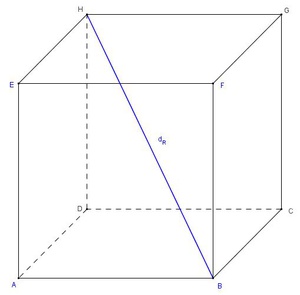
Zeichnet man eine beliebige Raumdiagonale des Würfels ein (z.B. jene vom Eckpunkt B zum Eckpunkt H), so entsteht ein rechtwinkeliges Dreieck (rechter Winkel im Eckpunkt D).

In jedem rechtwinkeligen Dreieck gilt der Lehrsatzes des Pythagoras, somit kann man mit dessen Hilfe die Länge der Raumdiagonale berechnen.

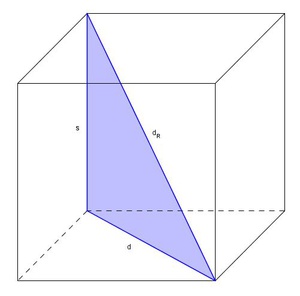
Die Raumdiagonale 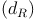(d_R) ist die Hypotenuse (=längste Seite) des rechtwinkeligen Dreiecks, die Kante (s) sowie die Flächendiagonale (d) bilden die Katheten (= kürzeren Seiten). Daher gilt:

$\text{Hypotenuse} = \sqrt {\text{Kathete\ hoch\ 2} + \text{Kathete\ hoch\ 2}}$

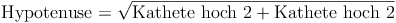
Wir setzen nun die Bezeichnungen in die Formel ein: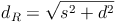
$d_R = \sqrt{s^2 + d^2}$

Die Flächendiagonale d kann folgendermaßen berechnet werden:
$d = \sqrt{s^2 + s^2}$
d^2 = s^2 + s^2

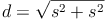
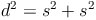
Für 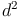d^2 wird nun also s^2 + s^2 eingesetzt:
$d_R = \sqrt{s^2 + s^2 + s^2}$

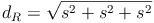
Nun kann noch addiert werden: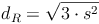
$d_R = \sqrt{3 \cdot s^2}$

Partielles (= teilweises) Wurzelziehen: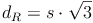
$d_R = s \cdot \sqrt{3}$

Raumdiagonale eines Würfels:

In einem Würfel sind alle Seiten gleich große Quadrate, daher sind auch alle Raumdiagonalen gleich lang und werden mit 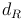bezeichnet.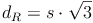

$d_R = s \cdot \sqrt{3}$

Dieser Artikel hat mir geholfen. das half mir
... leider nicht ... leider nicht
Kommentar Kommentar
3,3
423 Bewertungen

Kommentar #40508 von Luana 12.12.17 16:41 Luana: Aber wo ist der Unterschied zwischen einer Raumdiagobale und einer Flächendiagonale ?
Kommentar #42750 von pythagoras 04.07.19 01:36 pythagoras: fläche 2 dimensional
raum 3 dimensional
Kommentar #46814 von Inshallah 13.02.22 11:23 Inshallah: Hat mir gut geholfen
Kommentar #48229 von Alhamdulillah 14.12.23 20:41 Alhamdulillah: Sehr hilfreich!
Kommentar #48303 von Sam 23.01.24 13:30 Sam: Hat mir durch die 6 Klasse geholfen
Kommentar #48310 von Lev 26.01.24 10:18 Lev: Hat mir sehr geholfen
Kommentar #48612 von Lev 30.05.24 08:18 Lev: Hat mir sehr geholfen

Raumdiagonale eines Würfels

Die Raumdiagonale(n) des Würfels

Berechnung der Raumdiagonale eines Würfels

Kommentar verfassen

Ähnliche Arbeitsblätter