Pythagoräische Zahlen
Sind die Seitenlängen eines rechtwinkligen Dreiecks natürliche Zahlen, so nennt man diese pythagoräische Zahlen.
Berechnen von pythagoräischen Zahlen:Um die Seitenlängen a, b und c eines rechtwinkligen Dreiecks zu berechnen und um pythagoräische Zahlen zu erhalten, verwendet man folgende Formeln:
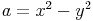
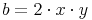
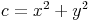
Bei den Varibalen a, b und c handelt es sich um die Seitenlängen des Dreiecks.
Bei den Varibalen x und y handelt es sich um beliebige natürliche Zahlen, wobei x > y sein muss.
Beispiel:
Wir wählen für  und für
und für 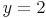
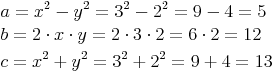
Alle 3 pythagoräische Zahlen zusammen sind ein pythagoräisches Zahlentripel
z.B.: 5, 12, 13
Einige pythagoräische Zahlentripel:z.B.: 5, 12, 13
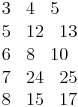
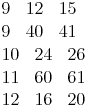
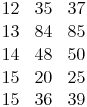
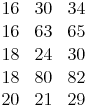
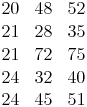
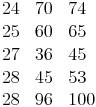
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Hope Aibangbee
Das ist nicht leicht