Gemischt periodische Dezimalzahlen

Gemischt periodische Dezimalzahlen in Brüche umwandeln

Gemischt periodische Dezimalzahlen in Brüche umwandeln

Die Anzahl der Dezimalstellen gibt den zu berechnenden x-Wert in Schritt 2 an.
2 Dezimalstellen = 100x , 3 Dezimalstellen = 1000x , ...

Die Anzahl der nicht-periodischen Dezimalstellen gibt den zu berechnenden x-Wert in Schritt 3 an.
2 Dezimalstellen = 100x , 3 Dezimalstellen = 1000x , ...

Beispiel: 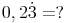0,2 \dot 3 = ?

Dezimalstellen: 2

Nicht-periodische Dezimalstellen: 1

1. Schritt: Zahl ausschreiben

x = 0,2 \dot 3

x = 0,233333...

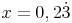
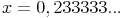
2. Schritt: 100x berechnen

x = 0,233333... / \cdot 100

100x = 23,333...

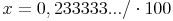
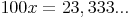
3. Schritt: 10x berechnen:

x = 0,233333... / \cdot 10

10x = 2,333...

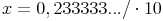
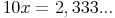
4. Schritt: Die beiden Gleichungen aus Schritt 2 und 3 subtrahieren

\begin{align} & \left. {\begin{matrix} 100x = 23,333... \\ \underline{\ 10x = \ 2,333... \end{matrix}}} \quad \right\} - \\ & { \quad 90x = 21,000...} \quad / : 90 \\ & x = \frac{21}{90} \\ \end{align}


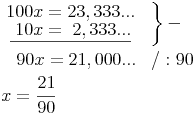
Gemischt periodische Dezimalzahlen in Brüche umwandeln:
(bei einer Dezimalzahl mit 2 Dezimalstellen, wobei die letzte davon periodisch ist)

1) Den Wert für 100x berechnen
2) Den Wert für 10x berechnen
3) Die beiden entstandenen Gleichungen subtrahieren
4) Den Wert für 1x ausdrücken (durch dividieren)
Kommentar #295 von Wastl 08.01.11 11:20
Wastl

Ihr müsst auch zeigen, wie man das umwandelt, wenn eine Zahl hinter dem Komma nicht zu der Periode gehört.

Kommentar #612 von Setare 30.08.12 21:44
Setare

Eine Zahl wie 1,2469469469… kann man damit auch nicht umwandeln…

Kommentar #1650 von Erich Hnilica, BEd 07.11.12 16:14
Erich Hnilica, BEd

@ Wastl:
Das wurde mit dem Beispiel demonstriert. Die Ziffer 2 steht hinter dem Komma und gehört nicht zur Periode!

@ Setare:
Deine Zahl ist keine gemischt-periodische Zahl und ist somit nicht Thema dieser Seite. Schau mal zwei Seiten weiter rauf (Allgemein)

Kommentar #7354 von Heinz 14.12.12 12:21
Heinz

Klar lässt sich auch 1,2469469 … so umwandeln, mit 10 und 10000 multiplizieren, die Gleichungen voneinander dividieren und als Bruch schreiben, 12457/9990 oder 1 2467/9990

Kommentar #9336 von Ronaldo 25.10.14 10:37
Ronaldo

danke war sehr behilflich, diese Seite ist saug geil ihr erklärt Beispiele einfach in Sekunden Schnelligkeit, einfach Super....

Kommentar #10118 von Der Ich 24.05.15 22:46
Der Ich

Oder einfach ausgedrückt:

x=[x*10^(n+1)-x*10^(n+1-N)]/[10^(n+1)-10^(n+1-N)]

n:= Anzahl der Dezimalstellen außerhalb der Periode
N:= Anzahl der Dezimalstellen innerhalb der Periode

Kommentar #27050 von Herbert 06.11.16 13:17
Herbert

Interessant wäre ein Beispiel mit 9 als letzte Zahl der Periode.
Da kommt man dann drauf, dass 0,9 periodisch gleich 1 sein muss.

Kommentar verfassen