Dezimalzahlen mit periodischen Dezimalstellen in Brüche umwandeln
Beispiel 1:
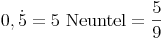
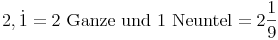
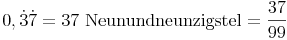
Dezimalzahlen mit periodischen Dezimalstellen in Brüche umwandeln:
Die periodische Ziffer wird in den Zähler geschrieben. Im Nenner schreibt man die Ziffer 9 so oft, wie es periodische Ziffern gibt.
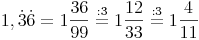
Die periodische Ziffer wird in den Zähler geschrieben. Im Nenner schreibt man die Ziffer 9 so oft, wie es periodische Ziffern gibt.
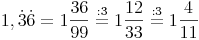
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Candy
Na ja hat mir aber NICHT geholfen..=(
ally
und wie geht das mit 0,2 Periode 9
Sari
Super hat mir nix geholfen wie geht zB: 4,1242424..
III
Hat mir geholfen !!! Vielen Dank :)
Martin
0,2 sind 2/10 oder 1/5
ines
ganz einfach 29/99
Leo
Ehm und wie geht das mit
beisp. 0,4 Periode 6?
RS
das funktioniert nicht mit 0,9 (9 periodisch)
Sally
Kein Wunder, weil 0,999... (Periode) gleich 1 ist. Dafür gibt es eine handvoll elementarer Beweise für die auch Schulmathematik ausreicht.
Beispiel: Durch schriftliche Division erhält man 1/9=0,1(periode). Aber 1/9*9=1, damit also 0,1(periode)*9=0,9(periode)=1/9*9=1.
Wer das ganze mathematischer betrachten möchte kann das analytisch über den Grenzwert oder die geometrische Reihe tun.
haha
Es hat mir geholfen danke
Ichhald
Doch das geht auch mit 0,999999 u.s.w
das ist nämlich 1
0,9999999...=1 und das ist nicht gerundet das ist ein mathematischer Fakt :)
Luciboy
War eine super hilfe!
destroyer
Hat mir richtig geholfen.Ich wusste net wie das geht und jetzt weiß ich es.Danke für die Erklärung
rim
Was ist 0,51 in einen Bruch umgewandelt
Björn Köhler
Es geht wunderbar und kürzt andere gängige Verfahren ab.
BisiBlaubeer
Sind -0,333333333 periode -10/3?
Ich checks einfach nicht.
aurel
Für alle Interessierten, die mehr über periodische rationale Zahlen wissen wollen, will ich hier ein paar Überlegungen zum Besten geben.
Eine Periode p wird von der Division durch die nächsthöhere Zehnerpotenz vermindert um 1 zum Ausdruck gebracht: Bei p = 45 -> 100 - 1 = 99
Nun will man p an einer beliebigen Nachkommastelle einsetzen lassen. n Verschiebungen nach rechts bedeuten eine Multiplikation mit 10^-n: 0,00345345.. = (345/999)*10^-2
Um vor die Periode eine beliebige Einleitung zu setzen geht man analog vor: 0,12345345 = 12/100 + (345/999)*10^-2
Licht ins Dunkle bringt ein Funktionsterm, der drei natürliche Zahlen a, b und p erhält und eine Rationale Zahl q auf sie abbildet:
q(a,b,p) = a + b/z(b) + p/(z(b)n(p))
a ... Vorkommazahl: int(q)
b ... Einleitung
p ... Periode
z(b) = 10^int(ld(b)+1) ... nächshöhere Zehnerpotenz
n(p) = z(p)-1 ... Äquivalent zu Absatz 2
int ... Ganzzahlfunktion: z.B.: int(3,4) = 3
ld ... Logarithmus zur Basis 10
Have fun~
LOLOLOLOLOLI
Super! Danke