Indirekt proportionale Zuordnungen (y = k/x)
Der Graph einer indirekt proportionalen Funktion ist ein Teil einer Hyperbel.
Beispiel:
Ein Bauarbeiter braucht für die Fertigstellung eines Kellers 10 Tage. Wie lange würden 2, 4 oder 5 Arbeiter für diese Arbeit benötigen? (Es wird angenommen, dass alle Bauarbeiter gleich viel arbeiten)
Stellen Sie die Abhängigkeit der Anzahl der Arbeiter zu der Arbeitszeit in Tagen a) in Form einer Tabelle, b) mit einer Formel und c) in einem Schaubild dar.
a) Tabelle:
Wir brauchen für dieses Beispiel eine Tabelle mit 2 Spalten: In einer Spalte steht die Anzahl der Arbeiter x, in der zweiten Spalte die Arbeitszeit t.
| Anzahl der Bauarbeiter x | Arbeitszeit t |
|---|---|
| 1 | 10 |
| 2 | 5 |
| 3 | 3.3 |
| 4 | 2.5 |
| 5 | 2 |
| ... | ... |
| x | 10/x |
b) Formel:
1 Bauarbeiter benötigt für diese Arbeit 10 Tage.
Teilen sich nun 2 Bauarbeiter diese Arbeit (also diese 10 Tage) gleichmäßig auf, so benötigen sie zusammen nur noch 5 Tage.
Teilen sich nun 3 Bauarbeiter diese Arbeit (also diese 10 Tage) gleichmäßig auf, so benötigen sie zusammen nur noch 3,3 Tage.
usw.
Die tatsächliche Arbeitszeit ergibt sich also, indem man die Arbeitszeit (10 Tage) auf die Anzahl der Arbeiter aufteilt (durch die Anzahl der Bauarbeiter dividiert):
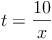
c) Schaubild:
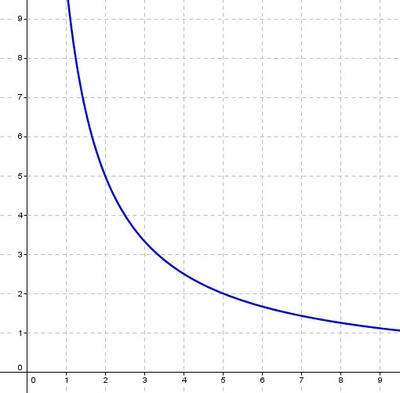
Für das Schaubild zeichnen wir ein kartesisches Koordinatensystem. Für die Zuordnung wird auf der x-Achse die Anzahl der Bauarbeiter x angegeben, auf der y-Achse die Arbeitszeit in Tagen t.
Indirekt proportionale ZuordnungenIndirekt proportionale Zuordnungen werden durch die Formel
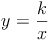ausgedrückt.wobei gilt:
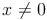
Das Schaubild (bzw. der Graph) einer indirekt proportionalen Zuordnung ist keine Gerade, sondern eine Kurve, die ein Teil einer Hyperbel ist.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Fineas
Das ist keine allgemeine Formel und kann man nicht in alle Bereiche anwenden. Es ist spezifisch nur für diesen Beispiel.
z.B. Gegeben ist eine Akku was unter 250mA Stromstärke, 13,5h für eine volle Aufladung benötigt. Wie lange benötigt dann die Akku unter 60mA für eine volle Ladung? Nach euren Prinzip würde die Formel t=13,5h / 60mA ausschauen. Also 0,225h? Nein!
Die allgemeine Formel ist dann in diesem Beispiel t=13,5h x 250mA / 60mA. Und das ergibt 56,25h und stimmt (je geringer der Strom, desto länger braucht man für eine volle Ladung)
In das oben genannte Beispiel wäre dann t= 1 x 10 / Anzahl der Mitarbeiter
Wobei 1 ist der benötigte Mitarbeiter für 10 Tage. Und wir können es weiterverwenden wenn z.B. für 10 Tage 2 Mitarbeiter notwendig sind. Wieviele Tage werden dann 5 Mitarbeiter brauchen?
Richtige Lösung: t= 2 x 10 / 5 = 4 Tage
Also: t = benötigte Mitarbeiter für y Tage multipliziert mit y (Tage) dividiert durch die Anzahl der Mitarbeiter (was gesucht ist)
Schöne Grüße aus Niederösterreich!