Die Flächendiagonalen eines Quaders
Eine Diagonale verbindet zwei gegenüberliegende Eckpunkte eines Rechtecks.
Die Oberfläche eines Quaders besteht aus 6 Rechtecken, von denen jeweils die beiden gegenüberliegenden Rechtecke kongruent (= deckungsgleich) sind.
Daher gibt es meist drei unterschiedlich lange Diagonalen im Quader: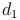 (Grund- und Deckfläche),
(Grund- und Deckfläche),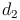 (vordere und hintere Seitenfläche),
(vordere und hintere Seitenfläche),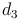 (linke und rechte Seitenfläche)
(linke und rechte Seitenfläche)
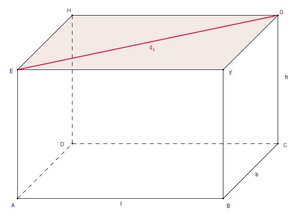
Berechnung der Flächendiagonale d1 eines Quaders
Zeichnet man die Flächendiagonale entweder auf der Grund- oder der Deckfläche eines Quaders ein, so teilt sie diese Seitenfläche in zwei gleich große rechtwinkelige Dreiecke.
In jedem rechtwinkeligen Dreieck gilt der Lehrsatzes des Pythagoras, somit kann man mit dessen Hilfe die Länge der Flächendiagonale berechnen.
Die Flächendiagonale 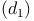 ist die Hypotenuse (=längste Seite) des rechtwinkeligen Dreiecks, die beiden Kanten (l und b) sind die Katheten (= kürzeren Seiten). Daher gilt:
ist die Hypotenuse (=längste Seite) des rechtwinkeligen Dreiecks, die beiden Kanten (l und b) sind die Katheten (= kürzeren Seiten). Daher gilt:
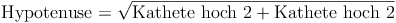
Wir setzen nun die Bezeichnungen in die Formel ein und erhalten: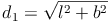
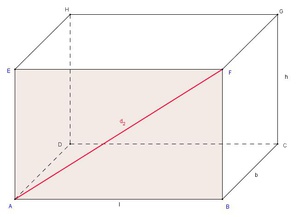
Berechnung der Flächendiagonale d2 eines Quaders
Zeichnet man die Flächendiagonale entweder auf der vorderen oder hinteren Seitenfläche eines Quaders ein, so teilt sie diese Seitenfläche in zwei gleich große rechtwinkelige Dreiecke.
In jedem rechtwinkeligen Dreieck gilt der Lehrsatzes des Pythagoras, somit kann man mit dessen Hilfe die Länge der Flächendiagonale berechnen.
Die Flächendiagonale 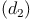 ist die Hypotenuse (=längste Seite) des rechtwinkeligen Dreiecks, die beiden Kanten (l und h) sind die Katheten (= kürzeren Seiten). Daher gilt:
ist die Hypotenuse (=längste Seite) des rechtwinkeligen Dreiecks, die beiden Kanten (l und h) sind die Katheten (= kürzeren Seiten). Daher gilt:
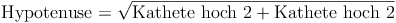
Wir setzen nun die Bezeichnungen in die Formel ein und erhalten: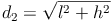
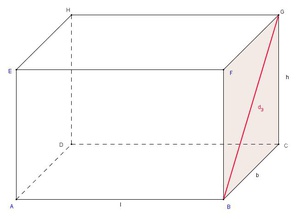
Berechnung der Flächendiagonale d3 eines Quaders
Zeichnet man die Flächendiagonale entweder auf der linken oder rechten Seitenfläche eines Quaders ein, so teilt sie diese Seitenfläche in zwei gleich große rechtwinkelige Dreiecke.
In jedem rechtwinkeligen Dreieck gilt der Lehrsatzes des Pythagoras, somit kann man mit dessen Hilfe die Länge der Flächendiagonale berechnen.
Die Flächendiagonale 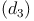 ist die Hypotenuse (=längste Seite) des rechtwinkeligen Dreiecks, die beiden Kanten (b und h) sind die Katheten (= kürzeren Seiten). Daher gilt:
ist die Hypotenuse (=längste Seite) des rechtwinkeligen Dreiecks, die beiden Kanten (b und h) sind die Katheten (= kürzeren Seiten). Daher gilt:
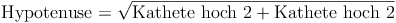
Wir setzen nun die Bezeichnungen in die Formel ein und erhalten: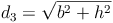
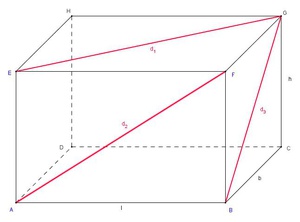
In einem Quader gibt es meist 3 unterschiedlich lange Flächendiagonalen:
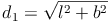
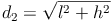
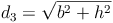
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Lukas
Man müsste etwas suchen aber dann fand ich was ich suchte obwohl ich es statt l Mi a kenne aber ich hab gefunden was ich gesucht habe
Finder
Lukas was meinst du ?