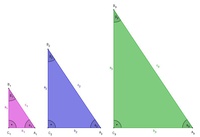
Ähnliche Figuren
Beispiel:
Konstruieren Sie ein rechtwinkeliges Dreieck, dessen Katheten 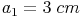 und
und 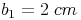 lang sein sollen.
lang sein sollen.
Als nächstes konstruieren Sie das gleiche Dreieck nochmals, allerdings mit doppelt so langen Kathetenlängen.
Schließlich konstruieren Sie das erste Dreieck nochmals, diesmal sollen die Katheten dreimal so lange sein.
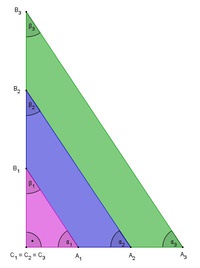
Wir legen die drei Dreiecke nun übereinander, um die Seiten und Winkel besser miteinander vergleichen zu können.
Winkel:
Wir messen nun alle Winkel der drei Dreiecke nach.
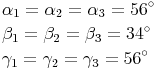
Einander entsprechende Winkel sind also gleich groß.
Seiten:
Wir messen nun alle Seiten der drei Dreiecke nach.
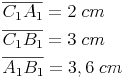
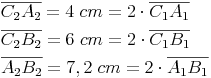
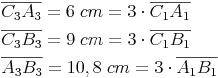
Ähnliche Figuren:
Ähnliche Figuren haben dieselbe Gestalt, sind aber unterschiedlich groß. Für ähnliche Figuren verwendet man folgendes Zeichen: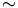
Sind ähnliche Figuren auch gleich groß, so handelt es sich um kongruente Figuren. Die Kongruenz ist also ein Sonderfall der Ähnlichkeit.
Entsprechende Winkel ähnlicher Figuren sind gleich groß.
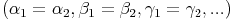
Entsprechende Seiten ähnlicher Figuren sind proportional zueinander (haben das gleiche Verhältnis).
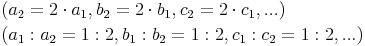
Ähnliche Figuren haben dieselbe Gestalt, sind aber unterschiedlich groß. Für ähnliche Figuren verwendet man folgendes Zeichen:
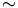
Sind ähnliche Figuren auch gleich groß, so handelt es sich um kongruente Figuren. Die Kongruenz ist also ein Sonderfall der Ähnlichkeit.
Entsprechende Winkel ähnlicher Figuren sind gleich groß.
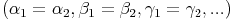
Entsprechende Seiten ähnlicher Figuren sind proportional zueinander (haben das gleiche Verhältnis).
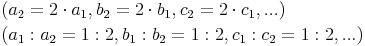
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar