Der Flächeninhalt des Dreiecks - Umkehraufgaben
Von einer Umkehraufgabe sprechen wir, wenn der Flächeninhalt des Dreiecks gegeben und die Seitenlänge bzw. die Höhe zu berechnen ist.
Man muss nun die Flächeninhaltsformel so umformen, dass man sich die fehlende Größe (die Seitenlänge bzw. die Höhe) berechnen kann.
Beispiel:
Ein Dreieck hat einen Flächeninhalt von 102 cm² und eine Höhe auf c von 12 cm. Berechne die Länge der Seite c!
Herleitung der Formeln
Aus dem Kapitel wissen wir bereits, dass der Flächeninhalt des Dreiecks mit "Seite mal zugehöriger Höhe dividiert durch 2" berechnet werden kann.
Daraus ergeben sich folgende Formeln:
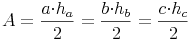
Nachdem wir in unserem Beispiel allerdings den Flächeninhalt des Dreiecks und die Höhe auf die Seite c kennen, nicht aber die Seite c, müssen wir die Formel so umformen, dass c alleine auf einer Seite steht:
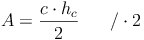
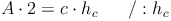
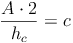
Beispiel (Fortsetzung)
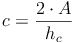
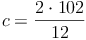
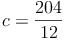
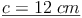
Antwort:
Die Seite c des Dreiecks ist 17 cm lang.
Weitere Formeln:
Analog zur Herleitung der Formel zur Berechnung der Seite c lässt sich die Grundformel auch so umformen, dass man die Seite a und b bzw. die Höhen ha, hb oder hc berechnen kann:
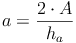
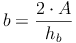
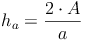
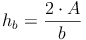
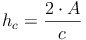
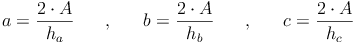
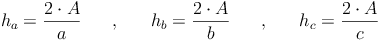
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
nele
mir hat diese Website sehr geholfen
Schweizer Sek A Schüler
Sehr hilfreich. Vielen Dank!!
Akunna Usuwa
mir hat diese website gefallen,Danke.