Reelle Zahlen
Die Menge der reellen Zahlen stellt eine Erweiterung
- der rationalen Zahlen
(Zahlen, die als Brüche dargestellt werden können) - um die Menge der irrationalen Zahlen dar
(Zahlen, die nicht als Bruch dargestellt werden können)
Man kann also schreiben:
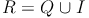
Die Menge der reellen Zahlen ist die Menge der rationalen Zahlen vereinigt mit der Menge der irrationalen Zahlen.
Reelle Zahlen - Abgeschlossene Operationen
Im Zahlenraum der reellen Zahlen sind die vier Grundrechnungsarten abgeschlossen.
Weiters ist das Wurzelziehen für positive reelle Zahlen (R+) abgeschlossen. Damit auch das Wurzelziehen von negativen Zahlen abgeschlossen ist, ist die Erweiterung zu den komplexen Zahlen
notwendig.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
hans kans
der erste satz ist nichtmal deutsch