Flächenberechnung beim regelmäßigen Sechseck
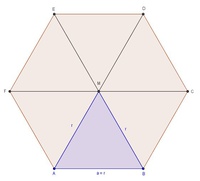
Um die Flächeninhaltsformel für das regelmäßige Sechseck herzuleiten zeichnen wir die 3 Diagonalen (AD, BE und CF) ein.
Die Diagonalen teilen die Figur in sechs gleich große gleichseitige Dreiecke.
Um den Flächeninhalt des regelmäßigen Sechsecks zu berechnen, berechnet man zuerst den Flächeninhalt eines gleichseitigen Dreiecks. Da alle sechs gleichseitige Dreiecke gleich groß sind, multipliziert man das Ergebnis anschließend mit 6, um auf den Flächeninhalt des regelmäßigen Sechsecks zu kommen.
Flächeninhalt des gleichseitigen Dreiecks:
Aus einem vorhergehenden Kapitel wissen wir bereits die Flächeninhaltsformel für das gleichseitige Dreieck.
In einem regelmäßigen Sechseck sind die Seitenlängen der sechs gleichseitigen Dreiecke der Radius r bzw. die Seitenlänge a des Sechsecks.
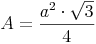
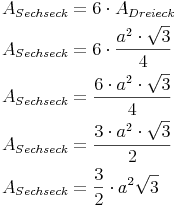
Nachdem es sich um 6 gleichseitige Dreiecke handelt, berechnen wir den Flächeninhalt von 1 gleichseitigen Dreieck und multiplizieren ihn mit 6!
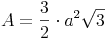
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Clemens
Warum zieht man die Wurzel aus 3 und rechnet durch 4?
Luchsen
"Aus einem vorhergehenden Kapitel wissen wir bereits die Flächeninhaltsformel für das gleichseitige Dreieck."
Siehe dort.
Schnabel
Der Flächeninhalt eines Dreiecks ist A*=h*a/2 mit der Höhe h = sin 60° (siehe gleichseitiges Dreieck) * a. Der Sinus von 60° ist (wurzel (3))/2. Die Wurzel kommt aus dem Sinus und die 4 von der Wurzel mal halbe Seitenlänge
Carste Stahl
Was ist denn bitte a ?
Wir machen gerade in Mathematik Projekt und brauchen es schnell.
Helmut
Es geht auch wesentlich einfacher. Um das Sechseck kann man ein Quadrat legen, dem 4 Dreiecke an den Ecken abgezogen werden müssen, welche wiederum zu 2 Rechtecken zusammengezogen werden können.
Sancho
Wenn man SW (Schlüsselweite)
als Bezug nimt, dann lautet
die Formel:
a • SW + 0,5 • a • sw, BZW.
A = aSW + o,5aSW
wobei a = SW • tan30
Sancho
Einfachste Formel für die Berechnung der Fläche eines
Sechsecks lautet:
A = 1,5 • a • b
wobei b = Mass des Sechskantes
Mario
Ich habe eine Frage an Sancho was ist denn b bzw kannst du mir das an einem bsp erklären wie ich auf b komme wäre sehr hilfreich wenn diese Formel stimmt
meru
ich check's nicht.
Chiara
Wie kann ich die Fläche von einem regelmäßigen sechseck berechnen wenn ich nur h gegeben habe?
Drömmler
Man muss doch doch die Dreiecke Innen zusammen Zählen, oder?
Chiara
Checke nicht Hhahaha ich schreibe einfach ab
Grandswiss
Ein Sechseck kann man in drei Teile teilen:
__ __
/ \ = /| + | | + |\
\__/ \| |__| |/
Ein Rechteck in der Mitte und je ein Dreieck links und rechts.
Die Fläche des Rechtecks in der Mitte sei a*b (a ist die Seitenlänge des Sechsecks und b die Höhe des Sechsecks)
Die zwei Dreiecke links und rechts kann man so zusammensetzen, dass ein Rechteck entsteht:
_
/| + |\ = | |
\| |/ |_|
Dieses Rechteck ist halb so gross wie das Rechteck in der Mitte = 0.5 * a*b.
Also alles zusammen a*b + 0.5 * a*b = 1.5 * a*b