Winkelberechnungen

Unbekannte Winkel von ebenen Figuren können durch Aufstellen einer Gleichung berechnet werden. Dazu ist es notwendig, dass man über die Winkelsumme und die Eigenschaften der Winkel der ebenen Figur Bescheid weiß.

Winkelberechnungen

Kennt man nicht die Größe aller Winkelb einer ebenen Figur, so kann man die fehlenden Winkel mit Hilfe von Gleichungen berechnen. Dazu ist es wichtig, die Winkelsumme der ebenen Figur zu kennen.

Je nach Anzahl der Eckpunkte haben ebene Figuren unterschiedliche Winkelsummen (= Summe aller Innenwinkel).

Winkelsummen:

Dreiecke: 180^\circ

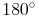
Vierecke: 360^\circ

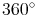
Fünfecke: 540^\circ

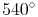
usw.

Beispiel:

In einem Parallelogramm ist der Winkel 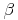\beta doppelt so groß wie der Winkel \alpha.

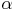Um dieses Beispiel lösen zu können, muss man einiges über die Winkelsumme des Parallelogramms wissen. Genauere Informationen finden Sie im Kapitel Die Winkel des Parallelogramms .

Überlegungen:

Ein Parallelogramm hat 4 Winkel, die Winkelsumme beträgt 360 Grad: 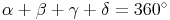\alpha + \beta + \gamma + \delta = 360^\circ

Der Winkel Beta ist doppelt so groß wie der Winkel Alpha: 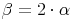\beta = 2 \cdot \alpha
Nun setzen wir in die Winkelsumme ein: 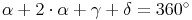\alpha + 2 \cdot \alpha + \gamma + \delta = 360^\circ

In einem Parallelogramm sind gegenüberliegende Winkel gleich groß: 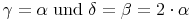\gamma = \alpha\ \text{und}\ \delta = \beta = 2 \cdot \alpha
Wir ersetzen Gamma: 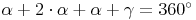\alpha + 2 \cdot \alpha + \alpha + \gamma= 360^\circ
Wir ersetzen Delta: 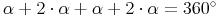\alpha + 2 \cdot \alpha + \alpha + 2 \cdot \alpha = 360^\circ

Nun lösen wir die Gleichung auf: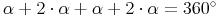
\alpha + 2 \cdot \alpha + \alpha + 2 \cdot \alpha = 360^\circ
6 \cdot \alpha = 360^\circ \qquad / : 6
\underline{\alpha = 60^\circ}

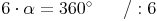
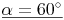
Zusammenfassung: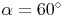

\alpha = 60^\circ
\beta = 2 \cdot \alpha = 2 \cdot 60^\circ = 120^\circ

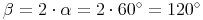
Antwort: In diesem Parallelogramm ist der Winkel Alpha 60° groß, der Winekl Beta 120° groß.

Winkelberechnungen:

Unbekannte Winkel von ebenen Figuren können durch Aufstellen einer Gleichung berechnet werden. Dazu ist es notwendig, dass man über die Winkelsumme und die Eigenschaften der Winkel der ebenen Figur Bescheid weiß.

Kommentar verfassen