Teilbarkeit durch 11
Für die Teilbarkeit durch 11 gibt es auch eine weitere Teilbarkeitsregel (mit nicht-alternierender 2er-Quersumme)
Wir zeigen Ihnen auf dieser Seite die aus unserer Sicht einfacherere Teilbarkeitsregeln durch 11 mit der alternierenden Quersummenregel.
Man erhält die alternierende Quersumme einer Zahl, indem man die Ziffern dieser Zahl abwechselnd addiert bzw. subtrahiert. Dabei kann sowohl von linke als auch von rechts begonnen werden.
Beispiel:
Prüfen Sie, ob die Zahl 104 654 durch 11 teilbar ist oder nicht.
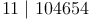 oder
oder 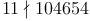 ?
?
Schritt 1:
Wir addieren die erste, dritte, fünfte, ... Ziffer: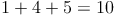
Schritt 2:
Wir addieren die zweite, vierte, sechste, ... Ziffer: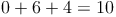
Schritt 3:
Um die alternierende Quersumme zu erhalten, subtrahiert man nun die zweite Summe von der ersten Summe. Ist das Ergebnis 0 oder durch 11 teilbar, dann ist die Zahl durch 11 teilbar: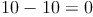
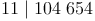
Eine Zahl ist durch 11 teilbar, wenn die alternierende Quersumme dieser Zahl durch 11 teilbar ist.
Dazu bildet man die Summe der ersten, dritten, fünften, ... Ziffer und die Summe der zweiten, vierten, sechsten, ...! Subtrahiert man beide Summen und erhält 0 oder eine andere durch 11 teilbare Zahl, so ist die Zahl durch 11 teilbar.
z.B.: 29678 ist durch 11 teilbar, weil:
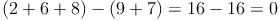
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Oliver
Hallo
das verstehe ich nicht, bzw. empfinde es widersprüchlich.
Einmal heißt es, wenn die alternierende Quersumme durch 11 teilbar ist, und ein andermal heißt es, wenn die alternierende Quersumme Null ergibt. Null ist nicht durch elf teilber, oder?
Oliver
Leni
Könnte man das ein bisschen kindlicher verfassen ?
Bitte!
Valetrino Tahlin
Ich fand die Website sehr hilfreich danke.
Georg Mendel
Sehr gut, merci. Finde ich super, wirklich!!
Fuldi
@Oliver: 0 ist durch 11 teilbar, denn 0 mal 11=0. Du meinst, glaub ich, dass 11 nicht durch 0 teilbar ist; das stimmt, macht aber nichts.
Maria M.
Ich war auch leicht irritiert wegen 0 und 11, als ich diesen Eintrag als Hilfe nutzte. Insbesondere der Satz "Ist das Ergebnis 0, dann ist die Zahl durch 11 teilbar" kann leicht irreführend (da ausschließlich klingend) sein. Die Regel ist auch anwendbar, wenn beispielsweise 11 herauskommt, wenn man beide Summen subtrahiert. Wie in dieser Aufgabe klar wird:
Let AB be a 2-digit integer such that the 8-digit number 4832AB18 is divisible by 11.
Find the maximum value of AB.
(Source: brilliant.org)
Albert Fiechter
4159*11=45749 Die alternierende Quersumme ist nicht null, aber durch 11 teilbar.
Ihr Mathelehrer
Hallo, danke fuer die Beschreibung. Ich verstehe es jetzt.
Alice Hermens
Ich habe den Eindruck, dass die Regel so zu verstehen ist: Entweder ist die alternierende Quersumme durch 11 teilbar oder es kommt eine 0 heraus, dann ist die Zahl durch 11 teilbar. Wenn man das mal systematisch durchgeht, dann merkt man dass das immer am Anfang des nächsten Hunderters mehr Zahlen werden, bei denen die 11 übrig bleibt. Bis 200 bleibt immer nur 0 übrig. Bei 209 bleibt 11 übrig, mit der 220 funktioniert aber wieder die Null als Rest (oder eben kein Rest). Die nächsten Zahlen die 11 als Rest haben sind die 308 und die 319, ab der 330 läuft alles wieder auf die Null. Dann kommt im 400er noch eine Zahl mehr herum bis die 440 erreicht ist (407,418 und die 429), usw.
Lisa
Zusammenfassend: Man bildet die alternierende Quersumme einer Zahl-
1. ERSTE! DRITTE FÜNFTE USW. ZIFFER ADDIEREN
2. ZWEITE! VIERTE SECHSTE USW. ZIFFER ADDIEREN
3.DAS 2. ERGEBNIS VOM ERSTEN ABZIEHEN
4. DAS ERGEBNIS MUSS GLEICH NULL SEIN! DANN IST DIE ZAHL DURCH 11 TEILBAr
Mathegenie
Das stimmt so nicht:
Nehmen wir die Zahl 269981, diese ist durch 11 teilbar. Aber verwendet man diese falsche Lösung, ergibt es keinen Sinn weil am Ende 3 rauskommt.
Mathegenie
Bitte das letzte komment wiederrufen!!! Hatte einen rechenfehler und es klappt doch! :D
Katharina Wieacker
Welche Schlüsse ziehe ich, wenn das Ergebnis eine negative Zahl ist? Mein Beispiel: Die Zahl 27675. Ich rechne (2+6+5)-(7+7)=13-14=-1 :-/
Danke im Voraus für die Antwort!
Katharina Wieacker
Kann es sein, dass bei der alternierenden Quersumme die kleinere Summe von der größeren Summe abgezogen werden muss?
Aramis
Es gibt einen Weg, der manchem hier leichter fallen könnte.
Zum Beispiel 104654:
Man trennt die hintere Ziffer 4 ab und erhält so zwei Zahlen, 10465 und 4. Von der ersten zieht man 4 ab und bekommt 10461.
Jetzt wiederholt man das bis zum Ende, kommt eine Zahl heraus, die durch 11 teilbar ist, ist die große Zahl auch durch 11 teilbar.
104654
10465-4=10461
1046-1=1045
104-5=99
99 ist durch 11 teilbar, also ist es 104654 auch :)
Jane
Alternierende Quersumme von 269981
-2+6-9+9-8+1=-3
Bzw
2-6+9-9+8-1=3
269981:11=24543,periode72