Zwei Kreise, die einander von außen berühren
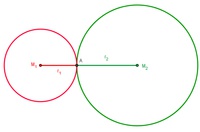
Zwei Kreise können so liegen, dass sie sich von außen in genau einem Punkt berühren. Dazu muss der Abstand der beiden Mittelpunkte der Kreise genauso groß sein wie der Radius des einen Kreises und der Radius des anderen Kreises zusammen.
2 Kreise können so zueinander liegen, dass sie sichin 1 Punkt von außen berühren.
Der Abstand der beiden Mittelpunkte muss genauso groß sein wie die Summe der beiden Radien:

Der Abstand der beiden Mittelpunkte muss genauso groß sein wie die Summe der beiden Radien:

Zwei Kreise, die einander von innen berühren
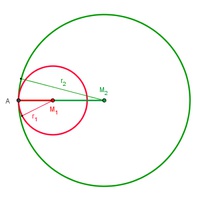
Zwei Kreise können so liegen, dass sie sich von innen in genau einem Punkt berühren. Dazu muss der Abstand der beiden Mittelpunkte der Kreise so groß sein wie der Radius des einen Kreises weniger dem Radius des zweiten Kreises.
2 Kreise können so zueinander liegen, dass sie sichin 1 Punkt von innen berühren.
Der Abstand der beiden Mittelpunkte muss der Radius des größeren weniger des kleineren Kreises betragen:

Der Abstand der beiden Mittelpunkte muss der Radius des größeren weniger des kleineren Kreises betragen:

- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Jyrki Reiner
mal ne andere frage: ist die größe des punktes, an dem sich die kreise berühren definierbar? ich bin der meinung, dass das nicht geht, da dieser punkt, bzw ein punkt im allgemeinen eindimensional ist und somit keine größe berechnet werden kann
Simone Kurnik
Es ist super zum lernen.