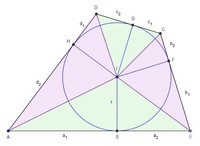
Der Flächeninhalt des Tangentenvierecks
Um die Formel für die Berechnung der Fläche eines Tangentenvierecks herleiten zu können, gehen wir von einem Tangentenviereck ABCD mit dem Inkreismittelpunkt I aus.
Die einzelnen Seiten teilen wir durch die Berührungspunkte mit dem Inkreis in jeweils zwei Abschnitte. Die Seite 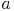 in die Abschnitte
in die Abschnitte 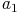 und
und 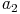 usw.
usw.
Wir wissen bereits aus dem vorhergehenden Kapitel, dass bezüglich der Seiten eines Tangentenvierecks folgendes gilt:
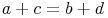
Verbinden wir nun den Inkreismittelpunkt mit jeweils 2 Eckpunkte, so entstehen folgende Dreiecke:
[ABI], [BCI], [CDI] und [DAI]
Jedes dieser Dreiecke hat dieselbe Höhe, nämlich den Inkreisradius r.
Da a + c = b + d gilt und alle Dreiecke dieselbe Höhe haben, müssen auch die jeweils gegenüberliegenden Dreiecke zusammen die gleiche Fläche aufweisen:
![[ABI] + [CDI] = [BCI] + [DAI] [ABI] + [CDI] = [BCI] + [DAI]](/media/formulas/f9ea848f2048ed72b065e43dd53873bd.png)
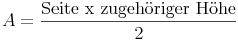
Linke Seite:![\begin{align}
& [ABI] + [CDI] = \frac{(a_1 + a_2) \cdot r}{2} + \frac{(c_1 + c_2) \cdot r}{2} = \\
& = \frac{(a_1 + a_2 + c_1 + c_2) \cdot r}{2} = \frac{(a + c) \cdot r}{2}
\end{align} \begin{align}
& [ABI] + [CDI] = \frac{(a_1 + a_2) \cdot r}{2} + \frac{(c_1 + c_2) \cdot r}{2} = \\
& = \frac{(a_1 + a_2 + c_1 + c_2) \cdot r}{2} = \frac{(a + c) \cdot r}{2}
\end{align}](/media/formulas/667a30c741e34584b0841a82d33bcbd0.png)
Rechte Seite:![\begin{align}
& [BCI] + [DAI] = \frac{(b_1 + b_2) \cdot r}{2} + \frac{(d_1 + d_2) \cdot r}{2} = \\
& = \frac{(b_1 + b_2 + d_1 + d_2) \cdot r}{2} = \frac{(b + d) \cdot r}{2}
\end{align} \begin{align}
& [BCI] + [DAI] = \frac{(b_1 + b_2) \cdot r}{2} + \frac{(d_1 + d_2) \cdot r}{2} = \\
& = \frac{(b_1 + b_2 + d_1 + d_2) \cdot r}{2} = \frac{(b + d) \cdot r}{2}
\end{align}](/media/formulas/c0b67b466a12d0224ff73bc9e37d7fa5.png)
Da wir ja wissen, dass a + c = b + d sind die Ergebnisse beider Seiten also identisch!
Um den Flächeninahlt des gesamten Tangentenvierecks ausrechnen zu können, können wir also eines der beiden Ergebnisse hernehmen und verdoppeln:
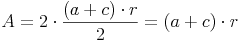
Ebenso können wir natürlich auch das andere Ergebnis hernehmen:
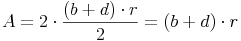
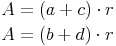
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar