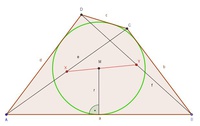
Newton's line
Benannt nach dem englischen Naturforscher Sir Isaac Newton stellt diese Gerade eine Besonderheit in jedem Tangentenviereck dar.
Um sie zu erhalten, konstruieren wir zunächst die beiden Diagonalen e (verbindet die gegenüberliegenden Eckpunkte A und c miteinander) und f (verbindet die gegenüberliegenden Eckpunkte B und D miteinander).
Nun halbieren wir die beiden Diagonalen und erhalten die beiden Halbierungspunkte X und Y. Verbinden wir diese beiden Punkte, so liegt der Mittelpunkt des Inkreises ebenfalls genau auf dieser Geraden.
Sollten Sie zwar den Inkreis eingezeichnet haben, die genaue Lage des Inkreismittelpunktes aber nicht kennen, so können Sie ihn ermitteln, indem sie eine Normale auf eine beliebige Seite auf den Berührungspunkt des Inkreises mit dieser Seite konstruieren. Der Inkreismittelpunkt ist der Schnittpunkt dieser Normalen mit der vorhin konstruierten Geraden.
In jedem Tangentenviereck liegen der Inkreismittelpunkt und die beiden Mittelpunkte der Diagonalen auf einer Geraden (= Newton's line).
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar