Parallelwinkel
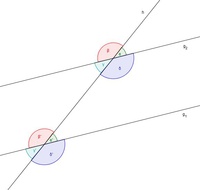
Wir konstruieren zwei parallele Geraden und benennen sie mit 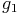 und
und 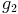 . Nun konstruieren wir eine >dritte Gerade, die die beiden parallelen Geraden scheidet und benennen diese mit
. Nun konstruieren wir eine >dritte Gerade, die die beiden parallelen Geraden scheidet und benennen diese mit 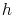 .
.
Wir bezeichnen die vier Winkel, die am Schnittpunkt der beiden Geraden 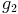 und
und 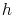 entstanden sind als
entstanden sind als![\alpha
\text{ [sprich: Alpha], }
\beta
\text{ [sprich: Beta], }
\gamma
\text{ [sprich: Gamma], }
\delta
\text{ [sprich: Delta]} \alpha
\text{ [sprich: Alpha], }
\beta
\text{ [sprich: Beta], }
\gamma
\text{ [sprich: Gamma], }
\delta
\text{ [sprich: Delta]}](/media/formulas/53f2d32d16dd3a516852a90139ca7bba.png) .
.
In unserem Beispiel können wir erkennen, dass die vier Winkel, die am Schnittpunkt der beiden Geraden 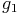 und
und 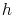 entstanden sind, gleich groß sind, wie die Ausgangswinkel:
entstanden sind, gleich groß sind, wie die Ausgangswinkel:
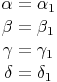
Sind die beiden Winkelschenkel jeweils parallel, so sind alle eingeschlossenen Winkel gleich groß.
Parallelwinkel:
Parallelwinkel sind Winkel, deren Schenkel jeweils parallel sind.
Deshalb sind Parallelwinkel auch jeweils gleich groß.
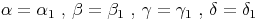
Parallelwinkel sind Winkel, deren Schenkel jeweils parallel sind.
Deshalb sind Parallelwinkel auch jeweils gleich groß.
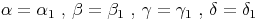
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Dilek
Das ist die tollste erfindung ich kann mir alles gut vorstellen und hoffentlich hilft das mir auch bei der Schularbeiten. Wenn ich eine 1 oder 2 kriege dank ich euch von ganzen Herzen. Hoffentlich griege ich eine 1
Anonym
Das hat sehr geholfen, es ist einfach sehr gut erklärt und ich hoffe es wird mir bei der Schularbeit,morgen helfen.
ich hoffe ich kriege eine 1 oder 2. Eine 1 wäre besser aber eine 2 ist auch nicht schlecht. : ) Vielen Dank !
Simon Gortana
nice