Die Zahl Pi
Aus dem vorherigen Kapitel wissen wir bereits, dass man immer denselben Wert erhält, wenn man den Umfang durch den Durchmesser eines Kreises dividiert. Dieser Wert liegt in etwa bei 3,14 und wird als Kreiszahl 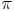 bezeichnet.
bezeichnet.
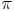 [sprich: pi] ist eine irrationale Zahl (eine nicht periodische Dezimalzahl mit unendlich vielen Dezimalstellen).
[sprich: pi] ist eine irrationale Zahl (eine nicht periodische Dezimalzahl mit unendlich vielen Dezimalstellen).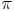 = 3,141592653...
= 3,141592653...
Geschichtliches über die Zahl Pi
Es gibt wohl kaum eine Zahl, die die Menschheit mehr beschäftigt hat, als die Kreiszahl Pi.
Archimedes gelang es bereits um 250 v. Chr. mit Hilfe des ein- und umgeschriebenen 96-Ecks die Zahl Pi abzuschätzen.
Erst 1766 konnte Johann Heinrich Lambert beweisen, dass Pi eine irrationale Zahl ist.
Heute ist die Zahl Pi von Supercomputern auf mehrere Billionen Dezimalstellen genau definiert.
Näherungsweise Herleitung der Zahl Pi
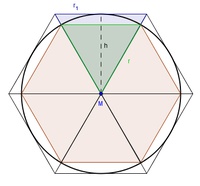
Wir konstruieren einen Kreis mit dem Radius r = 5 cm. Diesem wird z.B. ein regelmäßiges 6-Eck umgeschrieben und engeschrieben.
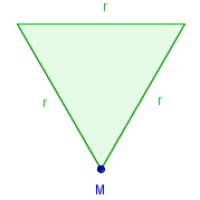
Verbindet man alle Eckpunkte mit dem Mittelpunkt M, so entstehen in jedem 6-Eck jeweils 6 gleichseitige Dreiecke.
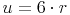
Umfang des umgeschriebenen 6-Ecks:
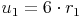
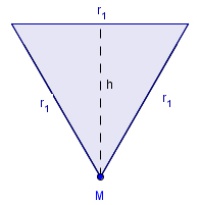
Weiters benötigen wir die Formel zur Berechnung der Höhe in einem gleichseitigen Dreieck:
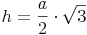
Aus der Skizze erkennen wir, dass die Höhe des umgeschriebenen 6-Ecks gleichzeitig der Radius des eingeschriebenen 6-Ecks ist, daher:
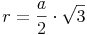
Außerdem haben wir die Seite a vorher als 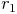 bezeichnet:
bezeichnet: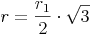
Wir formen so um, dass wir uns 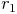 ausdrücken:
ausdrücken: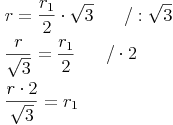
Dies setzen wir nun in die Formel 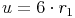 ein:
ein: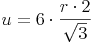
Die Kreiszahl Pi muss nun also zwischen dem Umfang des eingeschriebenen und des umgeschriebenen 6-Ecks liegen:
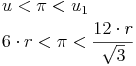
Wir wissen, dass der doppelte Radius den Durchmesser ergibt (2r = d):
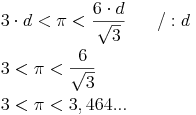
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Herzberger
Mein Kommentar war kein spam.
Ich habe nur auf einen Fehler hingewiesen.
Es wird in der Nachfolgezeile von
"Wir formen um...
statt durch Quadratwurzel durch 3 geteilt."
Erich Hnilica, BEd
Vielen Dank für die Info!
Der Fehler wurde bereits behoben.
PS: Unser System ist so eingestellt, dass alle neuen Beiträge von uns persönlich auf Spam überpürft werden. Deshalb kann es einige Zeit dauern, bis ein von dir verfasster Beitrag veröffentlicht wird - also auch wenn es sich um keinen Spam handelt!
Noah
Also eine Anleitung für GeoGebra wäre auch toll gewesen.
Müller
Wieso muss man zur Bestimmung von h bzw r, (a:2) mit Wurzel 3 multiplizieren? Wieso das Wurzel 3 heisst verstehe ich nicht...
Phil
Und warum setzt man jetzt die Formel u1=6*r1 ein ?
Helene
Irgendwie verstehe ich das mit dem Pi immer noch nicht. Wenn der Radius jetzt 4,5 cm ist und ich das Quadrat dieser Zahl mit 3,14 multipliziere kommt etwas falsches heraus.
kim
habe teilweise nichts verstanden...