Jahreszinsen für mehrere Jahre

Hier wird die Formel für die Berechnung von Jahreszinsen hergeleitet. Die KESt. (Kapitalertragsteuer) wird in diesem Kapitel nicht berücksichtigt.

Berechnung von Jahreszinsen

Wichtig:

Für die Berechnung der Jahreszinsen gehen wir in diesem Kapitel davon aus, dass:
- keine KESt. (Kapitalertragsteuer) zu bezahlen ist
- das Kapital für den gesamten Zeitraum unverändert bleibt, also die Sparzinsen am Jahresende stets abgehoben bzw. die Kreditzinsen am Jahresende stets einbezahlt werden.

Beispiel:

Ein Kapital von 2500 Euro wird mit 1,9% verzinst. Berechnen Sie die Jahreszinsen nach 1, 2, 3,  ..., t Jahren!

Jahreszinsen nach 1 Jahr:

Die Formel zur Berechnung der Jahreszinsen nach 1 Jahr kennen wir bereits aus dem vorherigen Kapitel:

Berechnung der Zinsen für 1 Jahr:

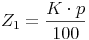
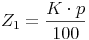
Z_1 = \frac{K \cdot p}{100}

Z_1 = \frac{K \cdot p}{100}

Z_1 = \frac{2500 \cdot 1,9}{100}

Z_1 = \frac{4750}{100}

\underline{Z = 47,50}

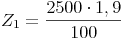
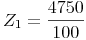
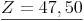
Zinsen nach mehreren Jahren:

Werden am Ende des 1. Jahres die Zinsen abgehoben, so wird nun im 2. Jahr wieder das Ausgangskapital (2500 Euro) verzinst.
Am Ende des 2. Jahres erhält man also dieselben Zinsen (47,50 Euro) wie am Ende des 1. Jahres.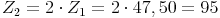

Z_2 = 2 \cdot Z_1 = 2 \cdot 47,50 = 95

Dasselbe gilt dann natürlich auch für das 3., 4., t. Jahr: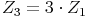

Z_3 = 3 \cdot Z_1

Z_4 =4 \cdot Z_1

Z_t = t \cdot Z_1

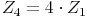
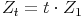
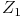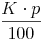Ersetzen wir nun in der letzten Formel Z_1 gegen \frac{K \cdot p}{100}, so erhalten wir:

Z_t = t \cdot \frac{K \cdot p}{100}

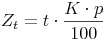
Nun können wir das t in den Zähler schieben: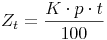

Z_t = \frac{K \cdot p \cdot t}{100}

Die Formel für die Berechnung von Jahreszinsen nach t Jahren lautet also: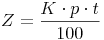

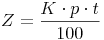
Z = \frac{K \cdot p \cdot t}{100}

Berechnung von Jahreszinsen nach mehreren Jahren:

Z = \frac{K \cdot p \cdot t}{100}

Zinsen = (Kapital x Zinssatz x Zeit ) : 100
Kommentar #43972 von anton Gschwantner 10.05.20 12:39
anton Gschwantner

ich bekomme heute 805 € , wie viel ist das seit 1987 ?

Kommentar #47626 von Lisbeth 14.12.22 19:36
Lisbeth

Und wie ist das nun mit der Zinseszins-Formel?
Dem Geld hinzugefügte Zinsen werden ja im 2ten Jahr auch verzinst.
Warum fällt das hier flach?
Oder habe ich was übersehen?

Liebe Grüße
Lisbeth

Kommentar verfassen