Flächeninhalt

Herleitung der Formel zur Berechnung des Flächeninhalts eines Deltoids

Der Flächeninhalt des Deltoids

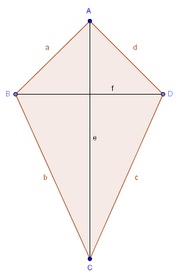
Herleitung der Flächeninhaltsformel:

1) Wir konstruieren ein beliebiges Deltoid.

2) Nun werden die Diagonalen e und f eingezeichnet.

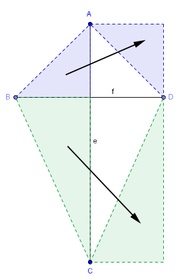
3) Die so entstandenen Dreiecke werden so "umgelegt" , dass die beiden linken Dreiecke auf der rechten Seite hinzugefügt werden.

4) Ein Rechteck ist entstanden, dessen Fläche noch immer so groß ist wie jene des ursprünglichen Deltoids.

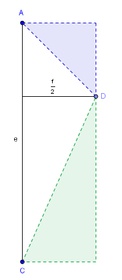
5) Berechnung der Fläche des Rechtecks:

${A{_R}=l{\cdot}b$

Die Länge des Rechtecks entspricht der Länge der Diagonale e, die Breite der halben Diagonale f:

${A{_R}=e{\cdot}\frac{f}{2}$

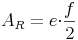
Eleganter geschrieben ergibt sich daraus:

${A{_R}=\frac{e{\cdot}f}{2}$

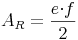
Die Fläche des Rechtecks ist genauso groß wie jene des Deltoids:

Flächeninhalt des Deltoids:

${A=\frac{e{\cdot}f}{2}$

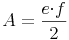
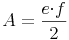
Flächeninhalt = (Diagonale e x Diagonale f) / 2