Flächeninhalt (mit Diagonalen)

Auf dieser Seite möchten wir Ihnen eine Formel herleiten, mit der Sie den Flächeninhalt einer Raute berechnen können, wenn die beiden Diagonalen e und f gegeben sind.

Den Flächeninhalt der Raute mit Hilfe der Diagonalen berechnen

Im vorhergehenden Kapitel haben wir Ihnen die Formel zur Berechnung des Flächeninhalts der Raute hergeleitet, wenn die Seitenlänge und die Höhe der Raute gegeben sind.

Auf dieser Seite möchten wir Ihnen eine Formel herleiten, mit der Sie den Flächeninhalt einer Raute berechnen können, wenn die beiden Diagonalen e und f gegeben sind.

Herleitung der Formel:

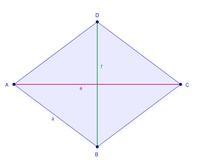
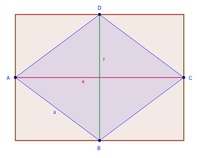
1) Wir konstruieren eine beliebige Raute

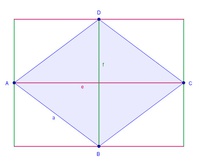
Der Flächeninhalt der Raute Der Flächeninhalt der Raute

2) Wir zeichnen rund um diese Raute ein Rechteck. Die Seiten des Rechtecks verlaufen parallel zu den Diagonalen und sind auch gleich lang wie die Diagonalen.

(l = e , b =  f)

Der Flächeninhalt der Raute Der Flächeninhalt der Raute

3) Das so entstandene Rechteck ist genau doppelt so groß wie die Raute. 

Der Flächeninhalt der Raute Der Flächeninhalt der Raute
Flächeninhalt eines Rechtecks:

Flächeninhalt = Seite mal Seite

4) Berechnung des Flächeninhalts des Rechtecks:

Die beiden Seiten des Rechtecks heißen e bzw. f, daher: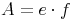

A = e \cdot f

6) Berechnung des Flächeninhalts der Raute:

Da die Raute genau halb so groß ist wie das Rechteck, ist auch der Flächeninhalt der Raute halb so groß wie jener des Rechtecks. Deshalb muss der Flächeninhalt des Rechtecks durch halbiert werden: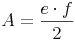

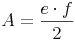
A = \frac{e \cdot f}{2}

Flächeninhalt der Raute:

A = \frac{e \cdot f}{2}

Flächeninhalt = (Diagonale e mal Diagonale f) dividiert durch 2

Beispiel:

Berechnen Sie den Flächeninhalt einer Raute mit den Diagonalen e = 7 cm und f = 6 cm!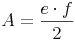

A = \frac{e \cdot f}{2}

A = \frac{7 \cdot 6}{2}

A = \frac{42}{2}

\underline{A = 21\ cm^2}

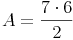
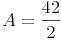
Antwort: Der Flächeninhalt der Raute beträgt 21 cm².

Kommentar #44188 von Peter Kaiser 24.06.20 14:32
Peter Kaiser

Ich suche die Fläche eines der beiden Dreiecke, die entstehen, wenn man die diagonal gegenüberliegenden Ecken eines Blatt Papiers aufeinander legt und die Falzkanten flach drückt. In meinem Fall hat das Rechteck die Abmessungen 150x200 mm.

Kommentar verfassen