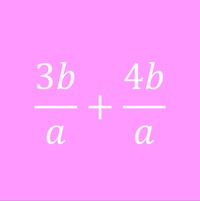Addieren und Subtrahieren von gleichnamigen Bruchtermen
Von gleichnamigen Bruchtermen spricht man dann, wenn die zu addierenden bzw. subtrahierenden Bruchterme denselben Nenner haben!
Aus dem Kapitel "Brüche" wissen wir bereits, dass man gleichnamige Brüche addiert bzw. subtrahiert, indem man die Zähler addiert bzw. subtrahiert und die Nenner unverändert lässt.
Beim Addieren und Subtrahieren gleichnamiger Brüche werden die Zähler addiert (subtrahiert) und die Nenner unverändert gelassen.
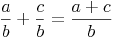
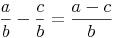
Dieses Wissen können wir auch auf Bruchterme anwenden. Auch hier ist es wichtig, dass die Nenner der beiden Brüche ungleich Null sind.
Bei den folgenden Beispielen setzen wir daher jeweils voraus, dass die Nenner der beiden Bruchterme ungleich Null sind!
Bsp. 1: Gleiche Variablen im Zähler werden addiert bzw. subtrahiert!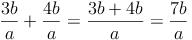
Bsp. 2: Hier kannst du im letzten Schritt auch noch kürzen!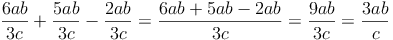
Bsp. 3: Ungleiche Variablen im Zähler dürfen natürlich NICHT addiert bzw. subtrahiert werden!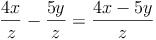
Bsp. 4: Achte beim Subtrahieren eines Bruches, dass der gesamte Bruch subtrahiert wird!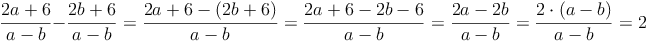
Beim Addieren und Subtrahieren gleichnamiger Bruchterme werden die Zähler addiert (subtrahiert) und die Nenner unverändert gelassen.
Bsp.:
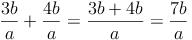
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar