Bevor wir uns dem Begriff "Definitionsmenge" widmen, müssen wir zuerst den Begriff "Grundmenge" eines Terms klären.
Grundmenge
Unter der Grundmenge eines Terms versteht man die Menge aller Zahlen, die man für die Variable (z.B. x) einsetzen darf.
Ist die Grundmenge z.B. die Menge der natürlichen Zahlen, so dürfen für die Variable(n) nur die Zahlen 1, 2, 3, 4, 5, ... eingesetzt werden.
Wenn als Grundmenge allerdings die Menge der ganzen Zahlen gewählt wurde, so dürfen die Zahlen ..., -4, -3, -2, -1, 0, 1, 2, 3, 4, ... für die Variable(n) eingesetzt werden.
Ist keine Grundmenge angegeben, so geht man von der umfassendsten Zahlenmenge, nämlich die Menge der reellen Zahlen, aus.
Definitionsmenge
Der Nenner eines Bruches darf nicht Null sein, da dies rechnerisch nicht lösbar wäre.
Somit müssen jene Zahlen der Grundmenge ausgeschlossen werden, die beim Ersetzen der Variablen bewirken würden, dass im Nenner Null steht.
Die Grundmenge ohne die ausgeschlossenen Zahlen heißt Definitionsmenge.
Beispiel 1:
Als Grundmenge wird die Menge der reellen Zahlen angenommen.
Die Definitionsmenge ist ebenso die Menge der reellen Zahlen, da keine Variable im Nenner vorkommt.
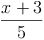

Beispiel 2:
Als Grundmenge wird die Menge der reellen Zahlen angenommen.
Die Definitionsmenge ist die Menge der reellen Zahlen, allerdings ohne der Zahl -3. Würde man für die Variable die Zahl -3 einsetzen, so wäre der Nenner Null.
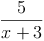
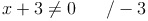
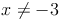
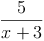
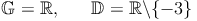
Der Backslash (\) steht hierbei für das Wort OHNE!
Beispiel 3:
Als Grundmenge wird die Menge der reellen Zahlen angenommen.
Die Definitionsmenge ist die Menge der reellen Zahlen, allerdings ohne der Zahlen -2 und +2. Würde man für die Variable die Zahl -2 oder +2 einsetzen, so wäre der Nenner Null.
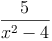
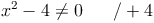
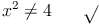
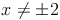
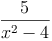

Der Nenner eines Bruches darf nicht Null sein, da dies rechnerisch nicht lösbar wäre.
Somit müssen jene Zahlen der Grundmenge ausgeschlossen werden, die beim Ersetzen der Variablen bewirken würden, dass im Nenner Null steht.
Die Grundmenge ohne die ausgeschlossenen Zahlen heißt Definitionsmenge.
z.B.:
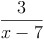
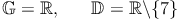
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar

