Dividieren von Bruchtermen

Bruchterme werden dividiert, indem man den ersten Bruchterm mit dem Kehrwert des zweiten Bruchterms multipliziert.

Dividieren von Bruchtermen

Aus dem Kapitel "Brüche" wissen wir bereits, dass man Brüche dividiert, indem man den ersten Bruch mit dem Kehrwert des zweiten Bruches multipliziert.

Tipp: Zwei Brüche werden multipliziert, indem man Zähler mit Zähler und Nenner mit Nenner multipliziert! (eventuell kann man davor auch noch kürzen!)

Dividieren von Brüchen:

Man dividiert einen Bruch durch einen anderen Bruch, indem man den 1. Bruch mit dem Kehrwert des 2. Bruches multipliziert.

\frac{a}{b} : \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c}

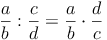
Tipp: Den Kehrwert erhält man durch Vertauschen von Zähler und Nenner!

Dieses Wissen können wir auch auf Bruchterme anwenden. Auch hier ist es wichtig, dass die Nenner der beiden Brüche ungleich Null sind.

Bei den folgenden Beispielen setzen wir daher jeweils voraus, dass die Nenner der beiden Bruchterme ungleich Null sind!

Bsp. 1: Dividend und Divisor sind Bruchterme: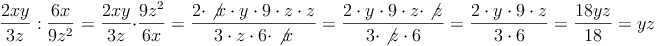

\frac{2xy}{3z} : \frac{6x}{9z^2} = \frac{2xy}{3z} \cdot \frac{9z^2}{6x} = \frac{2 \cdot \not{x} \cdot y \cdot9 \cdot z \cdot z}{3 \cdot z \cdot 6 \cdot \not{}x} = \frac{2 \cdot y \cdot9 \cdot z \cdot \not{z}}{3 \cdot \not{z} \cdot 6} = \frac{2 \cdot y \cdot9 \cdot z}{3 \cdot 6} = \frac{18yz}{18} = yz

Bsp. 2: Nur der Dividend ist ein Bruchterm: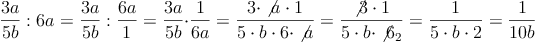

\frac{3a}{5b} : 6a = \frac{3a}{5b} : \frac{6a}{1} = \frac{3a}{5b} \cdot \frac{1}{6a} = \frac{3 \cdot \not{a} \cdot 1}{5 \cdot b \cdot 6 \cdot \not{a}} = \frac{\not{3} \cdot 1}{5 \cdot b \cdot \not{6}_2} = \frac{1}{5 \cdot b \cdot 2} = \frac{1}{10b}

Bsp. 3: Dividieren von Bruchtermen mit Summen und Differenzen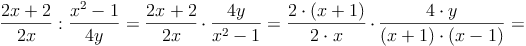

\frac{2x + 2}{2x} : \frac{x^2 - 1}{4y} = \frac{2x + 2}{2x} \cdot \frac{4y}{x^2 - 1} = \frac{2 \cdot (x + 1)}{2 \cdot x} \cdot \frac{4 \cdot y}{(x + 1) \cdot (x - 1)} =

= \frac{2 \cdot (x + 1) \cdot 4 \cdot y}{2 \cdot x \cdot (x + 1) \cdot (x - 1)} = \frac{(x + 1) \cdot 4 \cdot y}{x \cdot (x + 1) \cdot (x - 1)} = \frac{4 \cdot y}{x \cdot (x - 1)} = \frac{4y}{x(x - 1)}

Dividieren von Bruchtermen:

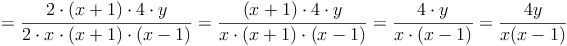
Bruchterme werden dividiert, indem man den ersten Bruchterm mit dem Kehrwert des zweiten Bruchterms multipliziert.

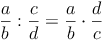\frac{a}{b} : \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} , wobei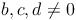 b, c, d \ne 0

Tipp: Den Kehrwert erhält man durch Vertauschen von Zähler und Nenner!

Kommentar verfassen