Bruchterme - Formelsammlung
Definition:
Kommen bei einem Term im Nenner Variable vor, so handelt es sich um einen Bruchterm.
z.B.: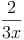 ,
, 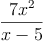
Kommen bei einem Term im Nenner Variable vor, so handelt es sich um einen Bruchterm.
z.B.:
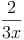 ,
, 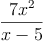
Definitionsmenge:
Der Nenner eines Bruches darf nicht Null sein, da dies rechnerisch nicht lösbar wäre.
Somit müssen jene Zahlen der Grundmenge ausgeschlossen werden, die beim Ersetzen der Variablen bewirken würden, dass im Nenner Null steht.
Die Grundmenge ohne die ausgeschlossenen Zahlen heißt Definitionsmenge.
z.B.: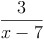
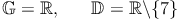
Der Nenner eines Bruches darf nicht Null sein, da dies rechnerisch nicht lösbar wäre.
Somit müssen jene Zahlen der Grundmenge ausgeschlossen werden, die beim Ersetzen der Variablen bewirken würden, dass im Nenner Null steht.
Die Grundmenge ohne die ausgeschlossenen Zahlen heißt Definitionsmenge.
z.B.:
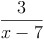
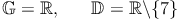
Erweitern von Bruchtermen:
Bruchterme werden erweitert, indem man Zähler und Nenner mit demselben Faktor (Zahl, Variable, Term) multipliziert.
z.B.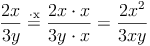
Bruchterme werden erweitert, indem man Zähler und Nenner mit demselben Faktor (Zahl, Variable, Term) multipliziert.
z.B.
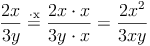
Kürzen von Bruchtermen:
Bruchterme werden gekürzt, indem man Zähler und Nenner durch demselben Faktor (Zahl, Variable, Term) dividiert.
z.B.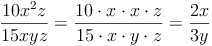
Bruchterme werden gekürzt, indem man Zähler und Nenner durch demselben Faktor (Zahl, Variable, Term) dividiert.
z.B.
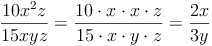
Multiplizieren von Bruchtermen:
Bruchterme werden multipliziert, indem man den Zähler mit dem Zähler und den Nenner mit dem Nenner multipliziert.
Beispiel:
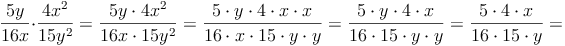
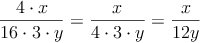
Tipps:
- Kürze immer so weit als möglich!
- Summen und Differenzen müssen vor dem Kürzen in Faktoren zerlegt werden!
Bruchterme werden multipliziert, indem man den Zähler mit dem Zähler und den Nenner mit dem Nenner multipliziert.
Beispiel:
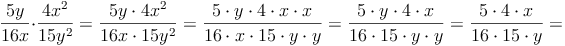
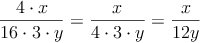
Tipps:
- Kürze immer so weit als möglich!
- Summen und Differenzen müssen vor dem Kürzen in Faktoren zerlegt werden!
Dividieren von Bruchtermen:
Bruchterme werden dividiert, indem man den ersten Bruchterm mit dem Kehrwert des zweiten Bruchterms multipliziert.
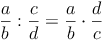 , wobei
, wobei 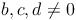
Tipp: Den Kehrwert erhält man durch Vertauschen von Zähler und Nenner!
Bruchterme werden dividiert, indem man den ersten Bruchterm mit dem Kehrwert des zweiten Bruchterms multipliziert.
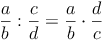 , wobei
, wobei 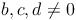
Tipp: Den Kehrwert erhält man durch Vertauschen von Zähler und Nenner!
Addieren und Subtrahieren von gleichnamigen Bruchtermen:
Beim Addieren und Subtrahieren gleichnamiger Bruchterme werden die Zähler addiert (subtrahiert) und die Nenner unverändert gelassen.
Bsp.: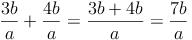
Beim Addieren und Subtrahieren gleichnamiger Bruchterme werden die Zähler addiert (subtrahiert) und die Nenner unverändert gelassen.
Bsp.:
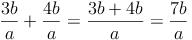
Addierenund Subtrahieren von ungleichnamigen Bruchtermen:
Um Bruchterme mit unterschiedlichen Nennern (= ungleichnamige Bruchterme) addieren oder subtrahieren zu können, müssen die Bruchterme zuerst auf den gleichen Nenner gebracht werden (= gleichnamig machen).
Anschließend werden die Zähler addiert (bzw. subtrahiert) und der Nenner unverändert gelassen.
Bsp.: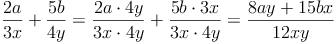
Um Bruchterme mit unterschiedlichen Nennern (= ungleichnamige Bruchterme) addieren oder subtrahieren zu können, müssen die Bruchterme zuerst auf den gleichen Nenner gebracht werden (= gleichnamig machen).
Anschließend werden die Zähler addiert (bzw. subtrahiert) und der Nenner unverändert gelassen.
Bsp.:
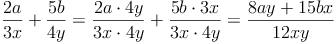
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar