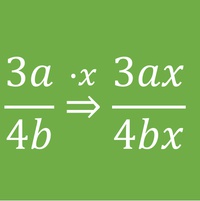Erweitern von Bruchtermen
Aus dem Kapitel "Brüche" wissen wir bereits, dass man Brüche erweitert, indem man den Zähler und den Nenner mit derselben Zahl (außer 0) mulipliziert.
Der Wert des Bruches ändert sich dadurch nicht!
Erweitern eines Bruches:
Der Wert eines Bruches bleibt gleich, wenn man Zähler und Nenner mit derselben Zahl multipliziert.
z.B. mit 3 erweitert ergibt
mit 3 erweitert ergibt  .
.
Der Wert eines Bruches bleibt gleich, wenn man Zähler und Nenner mit derselben Zahl multipliziert.
z.B.
 mit 3 erweitert ergibt
mit 3 erweitert ergibt  .
.
Dieses Wissen können wir auch auf Bruchterme anwenden. Auch hier ist es wichtig, dass der Erweiterungsterm ungleich Null ist.
Bei den folgenden Beispielen setzen wir daher jeweils voraus, dass der Nenner sowie der Erweiterungsterm ungleich Null sind!
Bsp. 1: Erweitern eines Bruchterms mit x: 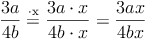
Bsp. 2: Erweitern eines Bruchterms mit y: 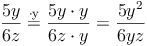
Bsp. 3: Erweitern eines Bruchterms mit (x - 2): 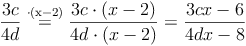
Erweitern von Bruchtermen:
Bruchterme werden erweitert, indem man Zähler und Nenner mit demselben Faktor (Zahl, Variable, Term) multipliziert.
z.B.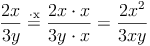
Bruchterme werden erweitert, indem man Zähler und Nenner mit demselben Faktor (Zahl, Variable, Term) multipliziert.
z.B.
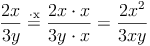
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar