Quadrat: Flächeninhalt - Umkehraufgaben

Ist der Flächeninhalt eines Quadrates bekannt, kann man sich die Seitenlänge sehr einfach berechnen. Dazu zieht man einfach die Quadratwurzel aus dem Flächeninhalt.

Berechnung der Seitenlänge s eines Quadrats, wenn der Flächeninhalt gegeben ist

Beispiel:
Von einem Quadrat ist der Flächeninhalt A = 225 cm² bekannt. Berechnen Sie die Seitenlänge des Quadrates!

Herleitung der Formel:
Aus dem vorherigen Kapitel wissen wir bereits, dass sich der Flächeninhalt eines Quadrats aus dem Produkt von Länge und Breite errechnet. Da Länge und Breite gleich lang sind, spricht man einheitlich von der Seitenlänge s:

Flächeninhalt des Quadrats:

A = s \cdot s
A = s^2

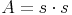
Wir müssen nun die Formel so umformen, dass wir eine Formel zur Berechnung der Seitenlänge s erhalten. Dazu muss s allein auf einer Seite stehen. Um dies zu erreichen, ziehen wir auf beiden Seiten die Quadratwurzel. Da das Quadrieren (²) und das Quadratwurzelziehen entgegengesetzte Rechenarten sind, heben sie sich auf und es bleibt auf der rechten Seite nur noch s übrig:

\begin{align} & A = s^2\qquad / \sqrt \\ & \sqrt {A} = s \\ \end{align}

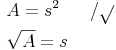
Beispiel (Forts.):

\begin{align} & s = \sqrt{A} \\ & s = \sqrt{225} \\ & s = 15\ cm \\ \end{align}

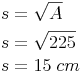
Probe: Wir setzen in die Flächeninhaltsformel ein

\begin{align} & A = s^2 \\ & A = s \cdot s \\ & 225 = 15 \cdot 15 \\ & 225 = 225 \\ \end{align}

Antwort:

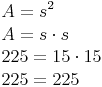
Das Quadrat hat eine Seitenlänge von 15 cm!

Berechnung der Seitenlänge eines Quadrats, wenn der Flächeninhalt gegeben ist

s = \sqrt{A}

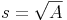
Seitenlänge = Quadratwurzel des Flächeninhaltes
Kommentar #26786 von Mathematical fool 03.11.16 14:09
Mathematical fool

Ok, also beim Flächeninhalt 16 wäre es folgend : (ich habe kein Wurzelzeichen--->wurzelzeichen =^ in dem Bsp,ok?)
SxS=16. |^
S= ^16
S=4cm( ungefähr) ?

Kommentar #40102 von Neue 13.09.17 13:54
Neue

Ich habe mir zwar des ganze Thema Quadratwurzel heute zum ersten mal angeschaut, würde aber auf das gleiche Ergebnis kommen wie du

Kommentar #47172 von Thomas 04.08.22 15:22
Thomas

Ich habe eine Fläche von 56 m x 20 m.
Das sind logischer weise 1120 m².
Will ich nun den Umfang errechnen, dann rechne ich (Wurzel aus 1120)x4.
Wurzel aus 1120 = 33,466
33,466 x 4 = 133,86 m Umfang.

ABER
Meine Werte waren 56,00 m x 20,00 m
Müsste sein: 56,00+56,00+20,00+20,00 = 152,00 m

Wo sind meine 18,14 m??????

Kommentar #47447 von Hallo2 09.11.22 16:32
Hallo2

Hallo Thomas,

Hier geht's um das Quadrat...die haben gleich lange Seiten.

Kommentar #48877 von Neugierig 07.11.24 13:11
Neugierig

Die Antwort auf die Frage von Thomas überzeugt mich nicht.
Wenn ich eine Fläche X habe, dann ist irrelevant, ob diese rechteckig oder quadratisch ist.
Alle Seitenlängen zusammengezählt müssen in beiden Fällen dasselbe ergeben.
Denn, ich kann ein Quadrat nehmen und auseinanderziehen, bekomme somit ein Rechteck, aber sowohl Fläche wie Gesamtlänge, verändern sich nicht.

Kommentar verfassen