Flächenberechnung Dreieck

Flächenberechnung des allgemeinen Dreiecks

Flächenberechnung Dreieck - Ableitung

Der Flächeninhalt eines Dreiecks lässt sich über die Flächeninhaltsformel eines Rechtecks herleiten. Diese lautet ja bekanntlich:

${A=a{\cdot}b}$
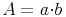
Fläche = Länge mal Breite

Allgemeines Dreieck (Konstruktion)

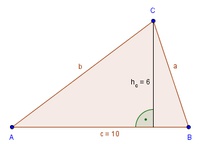
Wir konstruieren ein beliebiges Dreieck ABC:

(Alle Angaben in cm)

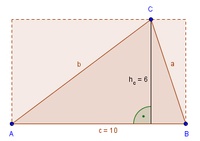
Nun ergänzen wir das Dreieck zu einem Rechteck.

Flächeninhaltsformel des Rechtecks:

${A_R=c {\cdot} h_c}$
Fläche = Länge mal Breite

Der Flächeninhalt des Dreiecks ist halb so groß wie der Flächeninhalt des Rechtecks. Daher lautet die Formel:

${A_D=\frac{c{\cdot}h_c}{2}=\frac{10{\cdot}6}{2}}=\frac{60}{2}=30 cm^2}$

Für jedes Dreieck gilt:

${A=\frac{a{\cdot}h_a}{2}=\frac{b{\cdot}h_b}{2}=\frac{c{\cdot}h_c}{2}}$
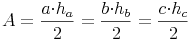
Fläche = (Seite x zugehöriger Höhe) / 2

Dreiecksfläche online berechnen

Seite c

c =

Höhe h_c

h_c =

Ergebnis: A = 237,5 cm²

(Wert gerundet auf 4 Dezimalstellen: 237,5000 cm²)

Der Lösungsweg im Detail:

Umrechnung Längenmaß

Schritt 1

Alle Angaben in gleiche Einheiten umwandeln

$c = 1.9\ \text{cm} = 1.9\ \text{cm}$

$h_c = 250.0\ \text{cm} = 250.0\ \text{cm}$

Schritt 2

Für die Berechnung des Flächeninhalts wird folgende Formel verwendet:

Flächenberechnung Dreieck

$A = \frac{c \cdot h_c}{2}$

Durch Einsetzen erhält man:

$A = \frac{1.9 \cdot 250.0}{2}$

$A = 237.5\ \text{cm²}^2$

Dieser Artikel hat mir geholfen. das half mir
... leider nicht ... leider nicht
Kommentar Kommentar
2,9
785 Bewertungen

Kommentar #7154 von Hakan 10.12.12 18:28 Hakan: Ich wusste es zwar schon, aber wollte sicher gehen. Danke an den verfasser.
Es half mir sehr!!
Kommentar #7156 von Hakan5851 10.12.12 18:32 Hakan5851: Also das hat mir geholfen
Kommentar #7622 von Jay-Dean 11.05.13 14:06 Jay-Dean: ich finde es gut dargestellt
Kommentar #8370 von mördi 12.01.14 21:44 mördi: hat mir sehr geholfen bei den hausaufgaben(:
Kommentar #9692 von xIKedech 11.02.15 21:10 xIKedech: Hat mir geholfen, danke :-)
Kommentar #10040 von Davidenco 06.05.15 19:08 Davidenco: Mit hat diese Website total viel geholfen. Vielen Dank für eure Arbeit die Ihr hier hinein gesteckt habt. :-)
Kommentar #12292 von Daniel 14.12.15 15:14 Daniel: Ein dreieck hat ja 3 seiten warum dann nur a.b
Kommentar #12516 von Johannes 09.01.16 20:29 Johannes: Ich bräuchte leider eine etwas andere formel da bei meiner rechnung nur die angabe C und die H steht aber danke Trotzdem :(
Kommentar #14230 von Nimo385i 07.04.16 20:40 Nimo385i: Es hat mir echt geholfen
Kommentar #38212 von Marvin 21.03.17 19:21 Marvin: Danke, diese Seite hat mir echt geholfen! Habe ich mir zu meinen Favoriten gemacht. :-) Wir schreiben nämlich morgen Mathe!
Viele Gruße,
Marvin
Kommentar #39380 von HANS KRUG 30.03.17 11:07 HANS KRUG: Abi vor 65 Jahren. die Formel war weg. Jetzt bin ich wieder dabei
Kommentar #39550 von Laura 02.05.17 16:28 Laura: Danke schön du hast mir sehr gut geholfen
Kommentar #39606 von Mülltonne 09.05.17 20:35 Mülltonne: Wir haben in der schule irgendwie das anders gemacht indem wir das dreieck doppelt genommen haben dann beide zusammengelegt zu einem Parallelogramm und dann ausgerechnet aber so wie hier ist es eigentlich viel einfacher nur die Frage ob ich auf diese Weise rechnen darf in der Arbeit
Kommentar #40070 von Fritz Dellbrügge 11.09.17 16:40 Fritz Dellbrügge: Super Erklärung
Besser und einfacher geht´s wirklich nicht.
Kommentar #40654 von Robsn 22.01.18 16:10 Robsn: Es half mir sehr aber die umkehrungs aufgaben kapier ich nicht
Kommentar #45308 von Ani 22.02.21 09:22 Ani: Bei mir stehen bei den Angaben g und h nicht a und b hat mir 0 geholfen lol

Flächenberechnung Dreieck

Flächenberechnung des allgemeinen Dreiecks