Flächenberechnung Rechtwinkeliges Dreieck

Herleitung der Formel zur Berechnung des Flächeninhalts eines rechtwinkeligen Dreiecks.

Flächenberechnung des rechtwinkligen Dreiecks

Der Flächeninhalt eines rechtwinkligen Dreiecks lässt sich über die Flächeninhaltsformel eines Rechtecks herleiten. Diese lautet ja bekanntlich:

${A=a{\cdot}b}$
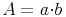
Fläche = Länge mal Breite

Zeichnet man die Diagonale des Rechtecks ein, so erhält man zwei deckungsgleiche rechtwinklige Dreiecke.

Der Flächeninhalt eines rechtwinkligen Dreiecks ist halb so groß wie der Flächeninhalt des Rechtecks.

Die Flächeninhaltsformel des Rechtecks muss also durch 2 dividiert werden.

Für jedes rechtwinklige Dreieck gilt:

${A=\frac{a {\cdot} b}{2}}$
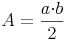
Flächeninhalt = (Kathete x Kathete) / 2

Seite a

a =

Seite b

b =

Seite c

c =

Zwei Seiten eines Dreiecks können nicht kürzer als die dritte Seite sein.

Kommentar #7634 von Ally 14.05.13 20:26 Ally: Diese Erklärung hat mir super gut geholfen! So konnte ich meine Hausaufgaben rasch lösen. Danke!
Kommentar #9600 von Gustav 04.01.15 12:02 Gustav: Der Beitrag ist nicht gut
Kommentar #39542 von Tom 01.05.17 16:53 Tom: Der ist hamma
Kommentar #40330 von KillerMaschine11 02.11.17 11:43 KillerMaschine11: Könnte man auch biiite die Umkehrformel beim Rechtwinligen Dreieck in die Website stellen ?
Kommentar #40674 von Mathematikerin (jedenfalls zukünftig) 24.01.18 17:27 Mathematikerin (jedenfalls zukünftig): Na ja, also, es war schon ganz gut, aber ich habe dadurch keine Hilfe bekommen - ich möchte wissen, wie viele rechtwinkligen Dreiecke man mit dem Flächeninhalt 6 cm² erhalten kann. Trotzdem danke!