Formelsammlung Pythagoräischer Lehrsatz
Der Satz des Pythagoras (= pythagoräischer Lehrsatz) ist der wohl berühmteste Lehrsatz für Berechnungen in der Geometrie und wurde nach Pythagoras von Samos benannt.
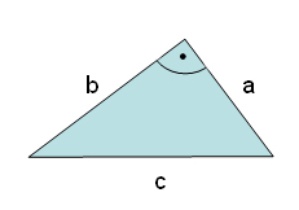
Dieser Lehrsatz gilt nur im rechtwinkeligen Dreieck. Die wichtigsten Formeln zu diesem Kapitel finden Sie in der folgenden Übersicht.
Bei unseren Formeln gehen wir davon aus, dass die beiden kürzeren Seiten (= Katheten) mit a und b sowie die längste Seite (= Hypotenuse) mit c bezeichnet werden.
Der Lehrsatz des Pythagoras:
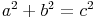
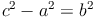
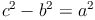
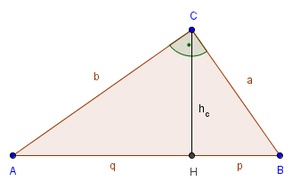
Seitenlängen berechnen:
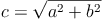
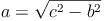
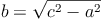
Für die Kathetensätze bzw. dem Höhensatz ist es wichtig zu wissen, dass die Höhe auf c (hc) die Hypotenuse c in zwei unterschiedlich lange Abschnitte teilt, die als p und q bezeichnet werden.
Kathetensätze bzw. Höhensatz:
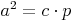
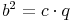
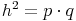
Diagonale eines Rechtecks:
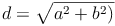
Diagonale eines Quadrates:
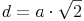
Flächendiagonalen eines Quaders:
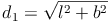
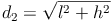
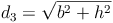
Raumdiagonale eines Quaders:
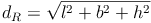
Flächendiagonale eines Würfels:
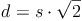
Raumdiagonale eines Würfels:
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar