Umfang eines Kreissektors (Kreisausschnittes)

Der Umfang eines Kreissektors (Kreisausschnittes) ist die Summe zweier Radien und des eingeschlossenen Kreisbogens.

Der Umfang eines Kreissektors

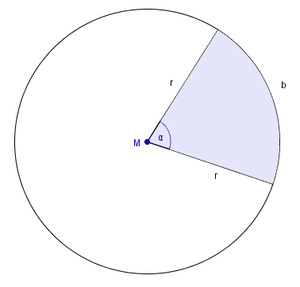
Ein Kreissektor (auch Kreisausschnitt genannt) ist ein Teil des Kreises, der von 2 Radien und einem Kreisbogen umgeben wird.

Der Umfang ist demnach die Summe zweier Radien und dem eingeschlossenen Kreisbogen.

Die Formel zur Berechnung eines Kreisbogens haben wir bereits im Kapitel "Bogenlänge" kennengelernt:

Wiederholung:
Berechnung der Bogenlänge eines Kreissektors (Kreisausschnitts):

b = \frac {r \cdot \pi \cdot \alpha}{180}

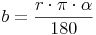
Bogenlänge = ( Radius mal Pi mal Zentriwinkel ) dividiert durch 180

Herleitung der Formel:

Der Umfang ist die Summe zweier Radien und dem eingeschlossenen Kreisbogen:
u = r + r + b

Die Summe der beiden Radien kann man auch als Multiplikation schreiben: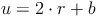
u = 2 \cdot r + b

Die Formel zur Berechnung der Bogenlänge kennen wir bereits aus einem vorhergehendem Kapitel. Wir setzen sie nun sfür b ein: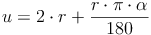
u = 2 \cdot r + \frac {r \cdot \pi \cdot \alpha}{180}

Beispiel:

Berechne den Umfang eines Kreissektors (Kreisausschnittes) mit dem Zentriwinkel 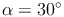\alpha = 30^\circ eines Kreises mit dem Radius r = 5 cm.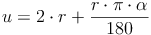

u = 2 \cdot r + \frac {r \cdot \pi \cdot \alpha}{180}

u = 2 \cdot 5 + \frac {5 \cdot \pi \cdot 30}{180}

u = 10 + \frac {150 \cdot \pi}{180}

u = 10 + 2,6

\underline{u = 12,6\ cm}

Umfang eines Kreissektors (Kreisausschnittes):

u = 2 \cdot r + \frac {r \cdot \pi \cdot \alpha}{180}

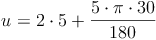
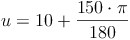
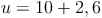
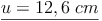
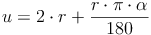
Umfang = 2 mal Radius plus Bogenlänge
Kommentar #42586 von Johannes Frewein 05.05.19 10:06
Johannes Frewein

Es hat mir sehr geholfen danke schön

Kommentar verfassen