Die Oberfläche der Kugel
Herleitung der Formel:
Für die Herleitung unserer Formel benötigen wir einen Tennisball. Dieser hat die Form einer Kugel und kann durch Auseinanderschneiden in 2 gleich große Halbkugeln geteilt werden.
1) Wir nehmen eine dieser Halbkugeln und stecken in den obersten Punkt eine Pinnadel.
2) Mit einer Wolle wickeln wir nun die Halbkugel kreisförmig bis zum unteren Ende ein und schneiden das Wollende ab.
3) Wir legen die Halbkugel auf ein Blatt Papier und zeichnen den Querschenittskreis 2 Mal nach.
4) Nun wickeln wir die Wolle von der Halbkugel ab.
5) Abschließend legen wir dieWolle nun so wie bei der Halbkugel - allerdings die Kreise aus.
Die Wolle, die zuerst die Halbkugel bedeckt hat, reicht nun für genau 2 Kreise, die denselben Radis haben wie jener der Kugel.
Macht man das mit beiden Halbkugeln (also der gesamten Kugel), so reicht die Wolle für 4 Kreise mit demselben Radius wie jener der Kugel.
Aus dem Kapitel "Kreis" kennen wir bereits die Flächeninhaltsformel zur Berechnung der Kreisfläche:
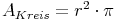
oder
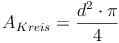
Nachdem sich die Oberfläche der Kugel in 4 Kreise legen lässt, müssen die Formeln mit 4 multipliziert werden:
Die Oberfläche der Kugel ist 4 Mal so groß wie der Flächeninhalt ihrer Großkreisfläche.
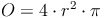
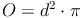
Beispiel 1:
geg.: Kugel: r = 8 cm
ges.: O
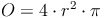
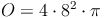
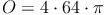
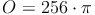
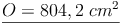
Beispiel 2:
geg.: Kugel: d = 10 cm
ges.: O
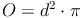
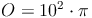
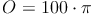
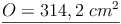
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar



Stefan Feuchtinger
gruselig