Die Höhe eines gleichseitigen Dreiecks mit Hilfe des pythagoräischen Lehrsatzes berechnen
Beispiel:
Von einem gleichseitigen Dreieck kennt man die Länge der Seite a = 7 cm. Berechnen Sie die Länge der Höhe h!
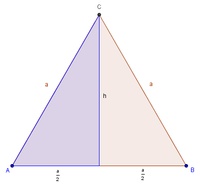
Zeichnet man die Höhe ein, so teilt diese das gleichseitige Dreieck in zwei gleich große rechtwinkelige Dreiecke.
In einem rechtwinkeligen Dreieck gilt der Lehrsatz des Pythagoras, daher gilt: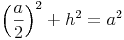
Wir formen um: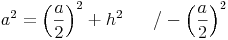
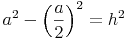
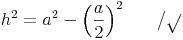
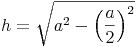
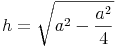
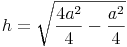
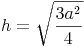
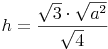
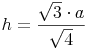
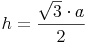
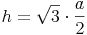
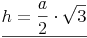
Beispiel (Forts.):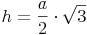
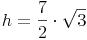
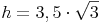
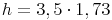
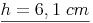
Antwort: Die Länge der Höhe h des gleichseitigen Dreiecks beträgt ca. 6,1 cm.
Die Höhe eines gleichseitigen Dreiecks berechnen:
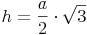
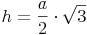
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
MatheGenius
Das half meinen Schülern sehr gut! Wir bauen es oft in unseren Unterricht ein.
Finn Zimmet
Sehr hilfreich, auch schon in der 8. Klasse. Hat mir den Arsch in der Mathearbeit gerettet. Danke dafür
MfG
Superdepp
Sehr Hilfreich, hat mir viel bei den Aufgaben geholfen!
Unknown
Ich würde gerne wissen wie ich die Höhe und die Seite a ausrechne wenn ich nur den Flächeninhalt gegeben habe also A? Finde das nirgends
Lena Till
Hi, ich weiß den Flächeninhalt des gliechseitigen Dreiecks zwar und der lautet:35cm², aber jetzt brauche ich die seitenlänge a , h und den Umfang