Umkehraufgabe: Die Höhe h eines Trapezes berechnen
Beispiel:
Von einem Trapez kennt man den Flächeninhalt A = 32 cm² sowie die Länge der Seite a = 10 cm und die Seite c = 4 cm. Berechnen Sie die Länge der Höhe h dieses Trapezes!
Herleitung der Formel:
Aus dem vorherigen Kapitel wissen wir bereits, dass sich der Flächeninhalt eines Trapezes aus der Hälfte der Summe der Seiten a und c multipliziert mit der Höhe h errechnet:
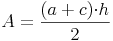
Nachdem wir den Flächeninhalt, die Länge der Seite a und die Länge der Seite c des Trapezes kennen, die Länge der Höhe h allerdings nicht, formen wir unsere Formel so um, bis die Höhe h allein auf einer Seite der Gleichung steht. Dazu multiplizieren wir zuerst beide Seite der Gleichung mit 2 und dividieren anschließend durch die Summe der Seiten a und c:
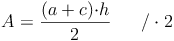
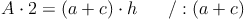
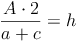
Beispiel (Forts.):
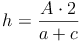
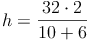
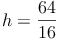
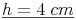
Antwort:
Die Länge der Höhe h beträgt 4 cm.
Probe: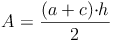
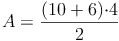
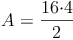
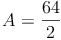
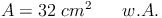
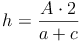
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
trollo pop
sehr schlecht szeniert
schlechte erklärungsversuche
am schlechtesten war die Übersicht
Max
Sei mal leise war mega gut erklärt du bist auch schlecht zensiert
Viola
Ich fands voll gut erklärt blos leider nich dis was ich gebraucht hab
Leon
Schlecht, was wenn man keinen Flächeninhalt hat?
ladybug
Ich fand es eigentlich auch ganz gut einfach nicht so gut ins detail. Also z.B hätten sie noch erklären könnten wieso man das so rechnet
layla
wusste nicht wo was erklärt wird
katharina
kann man h auch ohne flächeninhalt berechnen
Anonyme Hase
Gut erklärt,danke