Umkehraufgabe: Die Seite a eines Trapezes berechnen
Beispiel:
Von einem Trapez kennt man den Flächeninhalt A = 37,5 cm² sowie die Länge der Seite c = 4 cm und die Höhe h = 5 cm. Berechnen Sie die Länge der Seite a dieses Trapezes!
Herleitung der Formel:
Aus dem vorherigen Kapitel wissen wir bereits, dass sich der Flächeninhalt eines Trapezes aus der Hälfte der Summe der Seiten a und c multipliziert mit der Höhe h errechnet:
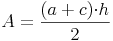
Nachdem wir den Flächeninhalt, die Länge der Seite c und die Länge der Höhe h des Trapezes kennen, die Länge der Seite a allerdings nicht, formen wir unsere Formel so um, bis die Seite a allein auf einer Seite der Gleichung steht. Dazu multiplizieren wir zuerst beide Seite der Gleichung mit 2, dividieren danach durch die Höhe h und subtrahieren abschließend die Seite c:
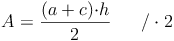
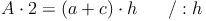
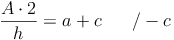
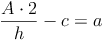
Beispiel (Forts.):
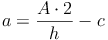
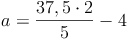
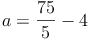
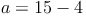
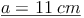
Antwort:
Die Länge der Seite a beträgt 11 cm.
Probe: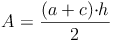
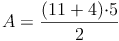
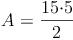
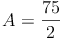
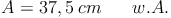
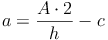
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar